题目内容
已知α、β是方程x2-
x=2=0的两实根,求log2
.
| 10 |
| α2-αβ+β2 |
| |α-β| |
考点:对数的运算性质
专题:函数的性质及应用
分析:首先根据一元二次方程求出α+β=
,α•β=2,进一步对关系式
进行恒等变换,最后求出结果.
| 10 |
| α2-αβ+β2 |
| |α-β| |
解答:
解:α、β是方程x2-
x=2=0的两实根
则:α+β=
α•β=2
=
=
=2
log2
=
故答案为:
| 10 |
则:α+β=
| 10 |
| α2-αβ+β2 |
| |α-β| |
| α2-αβ+β2 |
| |α-β| |
| (α+β)2-3αβ | ||
|
| 2 |
log2
| α2-αβ+β2 |
| |α-β| |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查的知识要点:一元二次方程的根和系数的关系,对数的运算和式子的恒等变形问题.

练习册系列答案
相关题目
设点(x0,0)在函数f(x)=sin(x-
)-1的图象上,其中
<x0<
,则cos(x0-
)的值为( )
| π |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
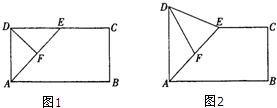 如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.
如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.