题目内容
已知f(x)=
(x≠-1).
(1)求f(x)的单调区间;
(2)证明对任意x>y>0,都有f(x+y)<f(x)+f(y).
| x |
| x+1 |
(1)求f(x)的单调区间;
(2)证明对任意x>y>0,都有f(x+y)<f(x)+f(y).
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用,不等式的解法及应用
分析:本题(1)通过变形得到相应的反比例函数的平移式,联系反比例函数的单调性,可得到本题结论; (2)通过对不等式右边的转化变形,利用放缩法,可得到本题结论.
解答:
(1)解:∵f(x)=
=1-
,
∵y=
仅有单调减区间为:(-∞,-1),(-1,+∞).
∴f(x)仅有单调增区间为:(-∞,-1),(-1,+∞).
(2)证明:对任意x>y>0,有:
f(x)+f(y)=
+
=
,
∴f(x+y)=
<
<f(x)+f(y).
∴原命题得证.
| x |
| x+1 |
| 1 |
| x+1 |
∵y=
| 1 |
| x+1 |
∴f(x)仅有单调增区间为:(-∞,-1),(-1,+∞).
(2)证明:对任意x>y>0,有:
f(x)+f(y)=
| x |
| x+1 |
| y |
| y+1 |
| 2xy+x+y |
| xy+x+y+1 |
∴f(x+y)=
| x+y |
| x+y+1 |
| xy+x+y |
| xy+x+y+1 |
∴原命题得证.
点评:本题考查了函数的单调性和不等式证明,本题有一定的思维量,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
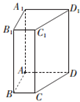 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.