题目内容
求函数y=log
(x2-3x+2)的单调区间.
| 1 |
| 2 |
考点:复合函数的单调性
专题:函数的性质及应用
分析:对数的真数大于0,求出函数的定义域,利用二次函数和复合函数的单调性即可得出单调区间.
解答:
解:要使函数y=log
(x2-3x+2)有意义,
则必须x2-3x+2>0,
解得x<1或2<x.
令u(x)=x2-3x+2,函数的对称轴为x=
,开口向上,
当x∈(-∞,1)时,函数u(x)单调递减,此时函数y=log
(x2-3x+2)单调递增;
当x∈(2,+∞)时,函数u(x)单调递增,此时函数y=log
(x2-3x+2)单调递减.
∴函数y=log
(x2-3x+2)单调递减区间是(2,+∞),单调递增区间是(-∞,1).
| 1 |
| 2 |
则必须x2-3x+2>0,
解得x<1或2<x.
令u(x)=x2-3x+2,函数的对称轴为x=
| 3 |
| 2 |
当x∈(-∞,1)时,函数u(x)单调递减,此时函数y=log
| 1 |
| 2 |
当x∈(2,+∞)时,函数u(x)单调递增,此时函数y=log
| 1 |
| 2 |
∴函数y=log
| 1 |
| 2 |
点评:本题考查了对数函数、复合函数的定义域、单调区间,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=log2(x+1)+alog2(1-x),且f(-x)=-f(x).
(1)求函数f(x)的解析式;
(2)求证:f(a)+f(b)=f(
)(-1<a<1,-1<b<1).
(1)求函数f(x)的解析式;
(2)求证:f(a)+f(b)=f(
| a+b |
| 1+ab |
函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(99)=( )
| A、13 | ||
| B、2 | ||
C、
| ||
D、
|
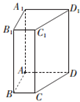 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.