题目内容
已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a2=5,则数列{an}的前n项和Sn为 .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出bn=n,an=2n+1,由此利用分组求和法能求出数列{an}的前n项和.
解答:
解:∵数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a2=5,
设bn=log2(an-1),
则b1=log2(3-1)=1,b2=log2(5-1)=2,
∴bn=n,∴log2(an-1)=n,∴an=2n+1,
∴数列{an}的前n项和:
Sn=2+22+23+…+2n+n
=
+n
=2n+1+n-2.
故答案为:2n+1+n-2.
设bn=log2(an-1),
则b1=log2(3-1)=1,b2=log2(5-1)=2,
∴bn=n,∴log2(an-1)=n,∴an=2n+1,
∴数列{an}的前n项和:
Sn=2+22+23+…+2n+n
=
| 2(1-2n) |
| 1-2 |
=2n+1+n-2.
故答案为:2n+1+n-2.
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
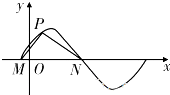 如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时
如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时 在△ABC中,点D在线段BC的延长线上,且
在△ABC中,点D在线段BC的延长线上,且