题目内容
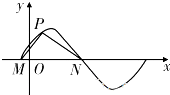如图所示，M，N是函数y=2sin（ωx+φ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时| PM |
| PN |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,平面向量数量积的运算
专题：三角函数的求值
分析：依题意知，点P（x0，y0）位于曲线最高点（此时y0=2）时，△MPN面积最大，利用△MPN为等腰直角三角形可求得|MN|=
•
=4，从而可得ω．
| 1 |
| 2 |
| 2π |
| ω |
解答：
解：由图知，当点P（x0，y0）位于曲线最高点（此时y0=2）时，△MPN面积最大，且
•
=0，
∴△MPN为等腰直角三角形，
设MN的中点为Q，则PQ⊥MN且|PQ|=
|MN|，即y0=
|MN|=2，
∴|MN|=4，又ω＞0，|MN|=
•
=4，
∴ω=
．
故答案为：
．
| PM |
| PN |
∴△MPN为等腰直角三角形，
设MN的中点为Q，则PQ⊥MN且|PQ|=
| 1 |
| 2 |
| 1 |
| 2 |
∴|MN|=4，又ω＞0，|MN|=
| 1 |
| 2 |
| 2π |
| ω |
∴ω=
| π |
| 4 |
故答案为：
| π |
| 4 |
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求得|MN|=4是关键，考查正弦的周期性及等腰直角三角形的性质的应用，属于中档题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
如图，圆柱内有一个三棱柱，三棱柱的底面在圆柱底面内，并且底面是正三角形，如果圆柱的体积是16π，底面直径与母线长相等．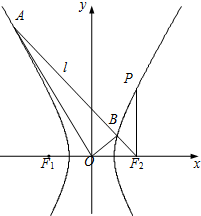
设点P在以F1、F2为左、右焦点的双曲线C：
已知函数f（x）=