题目内容
设g（x）是定义在R上，以1为周期的函数，若函数f（x）=x+g（x）在区间[2，3]上的值域为[-2，5]，则f（x）在区间[-2，6]上的值域为 ．
考点：函数的周期性,函数的值域
专题：函数的性质及应用
分析：根据g（x）是定义在R上，以1为周期的函数，得到g（x）=g（x+1），然后根据变量代换，逐步使变量取到给定的区间[-2，6]，最后求出不同区间段内的值域取并集即可．
解答：
解：因为g（x）是定义在R上，以1为周期的函数，
则g（x）=g（x+1）；
又因为f（x）=x+g（x）在区间[2，3]上的值域为[-2，5]，
令x+3=t，∵x∈[2，3]，∴t=x+3∈[5，6]，
则f（t）=t+g（t）=（x+3）+g（x+3）=（x+3）+g（x）=[x+g（x）]+3，
所以t∈[5，6]，f（t）∈[1，8]①．
再令x-4=t，∵x∈[2，3]，∴t=x-4∈[-2，-1]，
则f（t）=t+g（t）=（x-4）+g（x-4）=（x-4）+g（x）=[x+g（x）]-4，
所以t∈[-2，-1]，f（t）∈[-6，1]②．
综上，可得f（x）=x+g（x）在区间[-2，6]上的值域为[-6，8]．
故答案为：[-6，8]．
则g（x）=g（x+1）；
又因为f（x）=x+g（x）在区间[2，3]上的值域为[-2，5]，
令x+3=t，∵x∈[2，3]，∴t=x+3∈[5，6]，
则f（t）=t+g（t）=（x+3）+g（x+3）=（x+3）+g（x）=[x+g（x）]+3，
所以t∈[5，6]，f（t）∈[1，8]①．
再令x-4=t，∵x∈[2，3]，∴t=x-4∈[-2，-1]，
则f（t）=t+g（t）=（x-4）+g（x-4）=（x-4）+g（x）=[x+g（x）]-4，
所以t∈[-2，-1]，f（t）∈[-6，1]②．
综上，可得f（x）=x+g（x）在区间[-2，6]上的值域为[-6，8]．
故答案为：[-6，8]．
点评：本题主要考查了函数的周期性以及函数的值域的求法的运用，考查了学生的转化思想和能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
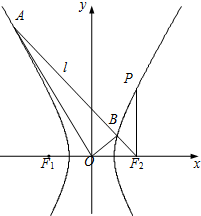设点P在以F1、F2为左、右焦点的双曲线C：