题目内容
已知a，b∈R，则“a=0”是“a+bi为纯虚数”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既非充分也非必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑,数系的扩充和复数
分析：根据复数的有关概念，以及充分条件和必要条件的定义进行判断．
解答：
解：当a=0，b=0时，a+bi为实数，不是纯虚数，充分性不成立，
若a+bi为纯虚数，则a=0，且b≠0，则必要性成立，
故“a=0”是“a+bi为纯虚数”必要不充分条件，
故选：C
若a+bi为纯虚数，则a=0，且b≠0，则必要性成立，
故“a=0”是“a+bi为纯虚数”必要不充分条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，根据复数的有关概念是解决本题的关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知cosα=-
，α∈（
，π），则cos（
+α）的值为（ ）
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
四面体ABCD中，AD与BC互相垂直，AD=2BC=4，且AB+BD=AC+CD=2
，则四面体ABCD的体积的最大值是（ ）
| 14 |
| A、4 | ||
B、2
| ||
| C、5 | ||
D、
|
下列选项中，说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、命题“若am2＜bm2，则a＜b”的逆命题是真命题 |
| C、命题“?x∈R，x2-x+1≥0”的否定是：“?x0∈R，x02-x0+1≤0” |
| D、命题“若x=y，则cosx=cosy”的逆否命题为真命题 |
已知正方体的棱长为1，且其顶点都在一个球面上，则该球的表面积为（ ）
| A、π | B、2π | C、3π | D、4π |
函数f（x）=
的导数是（ ）
| 1 |
| (3x-2)2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
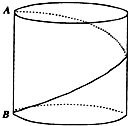如图，底面半径为1，高为2的圆柱，有A点有一只蚂蚁，现在这只蚂蚁要围绕圆柱由A点爬到B点，问蚂蚁爬行的最短距离是多少？