题目内容
某学校要从数学竞赛初赛成绩相同的四名学生(其中2名男生,2名女生)中,随机选出2名学生去参加决赛,则选出的2名学生恰好为1名男生和1名女生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:设2名男生用1,2表示,2名女生用3,4表示,首先列举随机选出2名学生的基本事件,再列举出满足出的2名学生恰好为1名男生和1名女生的基本事件,根据古典概型的概率公式计算即可.
解答:
解:设2名男生用1,2表示,2名女生用3,4表示,随机选出2名学生的基本事件(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6种,
选出的2名学生恰好为1名男生和1名女生的基本事件有(1,3),(1,4),(2,3),(2,4)共4种,
根据古典概率计算公式得选出的2名学生恰好为1名男生和1名女生的概率P=
=
.
故选:D.
选出的2名学生恰好为1名男生和1名女生的基本事件有(1,3),(1,4),(2,3),(2,4)共4种,
根据古典概率计算公式得选出的2名学生恰好为1名男生和1名女生的概率P=
| 4 |
| 6 |
| 2 |
| 3 |
故选:D.
点评:本题主要考查了古典概型的概率问题,关键是一一列举出满足条件的基本事件,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设{an}是等比数列,若a2=3,a7=1,则数列{an}前8项的积为( )
| A、56 | B、80 | C、81 | D、128 |
定义在R上的函数f(x)在(-∞,-2)上是减函数,且f(x-2)的图象关于y轴对称,则( )
| A、f(-3)<f(1) |
| B、f(-3)=f(0) |
| C、f(-3)=f(1) |
| D、f(-3)>f(0) |
若k>1,a>0,则k2a2+
取得最小值时,a的值为( )
| 16 |
| (k-1)a2 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
已知a,b∈R,则“a=0”是“a+bi为纯虚数”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既非充分也非必要条件 |
经过点(-1,0),且与直线x+2y-3=0垂直的直线方程是( )
| A、2x-y+2=0 |
| B、2x+y+2=0 |
| C、2x-y-2=0 |
| D、x-2y+1=0 |
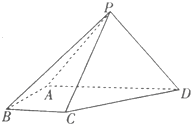 如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2
如图在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD=2,底面ABCD是直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2