题目内容
下列选项中，说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、命题“若am2＜bm2，则a＜b”的逆命题是真命题 |
| C、命题“?x∈R，x2-x+1≥0”的否定是：“?x0∈R，x02-x0+1≤0” |
| D、命题“若x=y，则cosx=cosy”的逆否命题为真命题 |
考点：四种命题
专题：简易逻辑
分析：根据四种命题之间的关系即可得到结论．
解答：
解：A．命题“若x2=1，则x=1”的否命题为：“若x2≠1，则x≠1”，故A错误．
B．命题“若am2＜bm2，则a＜b”的逆命题：若a＜b，则am2＜bm2，当m=0时，逆命题不正确，故B错误．
C．命题“?x∈R，x2-x+1≥0”的否定是：“?x0∈R，x02-x0+1＜0”，故C错误．
D．命题“若x=y，则cosx=cosy”为真命题，则它的逆否命题为真命题，故D正确．
故选：D
B．命题“若am2＜bm2，则a＜b”的逆命题：若a＜b，则am2＜bm2，当m=0时，逆命题不正确，故B错误．
C．命题“?x∈R，x2-x+1≥0”的否定是：“?x0∈R，x02-x0+1＜0”，故C错误．
D．命题“若x=y，则cosx=cosy”为真命题，则它的逆否命题为真命题，故D正确．
故选：D
点评：本题主要考查四种命题的真假判断，比较基础．
练习册系列答案
相关题目
已知集合A={y|x2+y2=1}，B={y|y=x}，则A∩B=（ ）
A、{（-
| ||||||||||||||||
B、{-
| ||||||||||||||||
| C、[-1，1] | ||||||||||||||||
| D、{-1，1} |
设△ABC的内角A，B，C所对的边分别是a，b，c，若sinA，sinC，sinB成等差数列，且3c=5a，则角B=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的函数f（x）在（-∞，-2）上是减函数，且f（x-2）的图象关于y轴对称，则（ ）
| A、f（-3）＜f（1） |
| B、f（-3）=f（0） |
| C、f（-3）=f（1） |
| D、f（-3）＞f（0） |
能正确表示图中阴影部分的选项为（ ）
| A、∁U（M∪N） |
| B、∁U（M∩N） |
| C、（M∪N）∩∁U（M∩N） |
| D、（M∩N）∪∁U（M∪N） |
已知a，b∈R，则“a=0”是“a+bi为纯虚数”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既非充分也非必要条件 |
已知a=（
）x，b=（
）x-1，c=log
x，且x＞1，则（ ）
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、b＞c＞a |
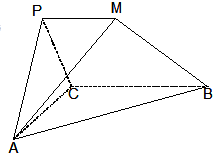在如图所示的多面体PMBCA中，平面PAC⊥平面ABC，△PAC是边长为2的正三角形，PM∥BC，且BC=2PM=4，AB=2