题目内容
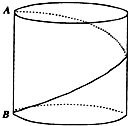如图，底面半径为1，高为2的圆柱，有A点有一只蚂蚁，现在这只蚂蚁要围绕圆柱由A点爬到B点，问蚂蚁爬行的最短距离是多少？考点：多面体和旋转体表面上的最短距离问题,旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：将圆柱侧面展开得到一个矩形，根据两点之间线段最短，求出对角线长即可．
解答：
解：因为圆柱底面圆的周长为2π，高为2，
所以将侧面展开为一长为12，宽为5的矩形，
根据勾股定理，对角线长为
=2
．
故蚂蚁爬行的最短距离为2
．
所以将侧面展开为一长为12，宽为5的矩形，
根据勾股定理，对角线长为
| (2π)2+22 |
| π2+1 |
故蚂蚁爬行的最短距离为2
| π2+1 |
点评：此题考查了圆柱的侧面展开图和勾股定理，需要同学们有一定的空间思维能力．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
已知a，b∈R，则“a=0”是“a+bi为纯虚数”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既非充分也非必要条件 |
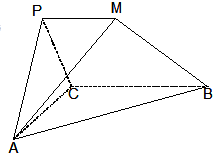在如图所示的多面体PMBCA中，平面PAC⊥平面ABC，△PAC是边长为2的正三角形，PM∥BC，且BC=2PM=4，AB=2
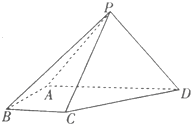如图在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，PA=PD=2，底面ABCD是直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2
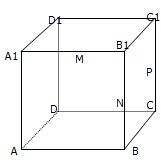如图，在棱长为1的正方形ABCD-A1B1C1D1中，M、N、P分别为A1B1、BB1、CC1的中点．