题目内容
四面体ABCD中，AD与BC互相垂直，AD=2BC=4，且AB+BD=AC+CD=2
，则四面体ABCD的体积的最大值是（ ）
| 14 |
| A、4 | ||
B、2
| ||
| C、5 | ||
D、
|
考点：棱柱、棱锥、棱台的体积
专题：
分析：作BE⊥AD于E，连接CE，说明B与C都是在以AD为焦距的椭球上，且BE、CE都垂直于焦距AD，BE=CE．取BC中点F，推出四面体ABCD的体积的最大值，当△ABD是等腰直角三角形时几何体的体积最大，求解即可．
解答：
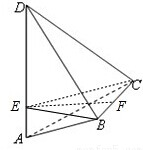解：作BE⊥AD于E，连接CE，则AD⊥平面BEC，所以CE⊥AD，
由题设，AB+BD=AC+CD=2
，所以B与C都是在以AD为焦点的椭圆上，且BE、CE都垂直于焦距AD，
因为AB+BD=AC+CD=2
，所以△ABD≌△ACD，所以BE=CE．
取BC中点F，所以EF⊥BC，EF⊥AD，四面体ABCD的体积的最大值，只需EF最大即可，
当△ABD是等腰三角形时几何体的体积最大，BE=CE=
，再求出EF=3，故可知答案为4，
故选A．
解：作BE⊥AD于E，连接CE，则AD⊥平面BEC，所以CE⊥AD，由题设，AB+BD=AC+CD=2
| 14 |
因为AB+BD=AC+CD=2
| 14 |
取BC中点F，所以EF⊥BC，EF⊥AD，四面体ABCD的体积的最大值，只需EF最大即可，
当△ABD是等腰三角形时几何体的体积最大，BE=CE=
| 10 |
故选A．
点评：本题考查棱柱、棱锥、棱台的体积，考查空间想象能力，逻辑推理能力以及计算能力．
练习册系列答案
相关题目
极坐标系内曲线ρ=2cosθ上的动点P与定点Q（1，
），的最近距离等于（ ）
| π |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知集合A={y|x2+y2=1}，B={y|y=x}，则A∩B=（ ）
A、{（-
| ||||||||||||||||
B、{-
| ||||||||||||||||
| C、[-1，1] | ||||||||||||||||
| D、{-1，1} |
设{an}是等比数列，若a2=3，a7=1，则数列{an}前8项的积为（ ）
| A、56 | B、80 | C、81 | D、128 |
设△ABC的内角A，B，C所对的边分别是a，b，c，若sinA，sinC，sinB成等差数列，且3c=5a，则角B=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的函数f（x）在（-∞，-2）上是减函数，且f（x-2）的图象关于y轴对称，则（ ）
| A、f（-3）＜f（1） |
| B、f（-3）=f（0） |
| C、f（-3）=f（1） |
| D、f（-3）＞f（0） |
已知a，b∈R，则“a=0”是“a+bi为纯虚数”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既非充分也非必要条件 |