题目内容
函数f（x）=
的导数是（ ）
| 1 |
| (3x-2)2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点：导数的运算
专题：导数的概念及应用
分析：根据复合函数的导数公式即可得到结论
解答：
解：∵f（x）=
，
∴f′（x）=-2（3x-2）-3•（3x-2）′=
，
故选：C．
| 1 |
| (3x-2)2 |
∴f′（x）=-2（3x-2）-3•（3x-2）′=
| -6 |
| (3x-2)3 |
故选：C．
点评：本题主要考查导数的计算，根据复合函数的导数公式是解决本题的关键．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知集合A={y|x2+y2=1}，B={y|y=x}，则A∩B=（ ）
A、{（-
| ||||||||||||||||
B、{-
| ||||||||||||||||
| C、[-1，1] | ||||||||||||||||
| D、{-1，1} |
已知a，b∈R，则“a=0”是“a+bi为纯虚数”的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既非充分也非必要条件 |
已知a=（
）x，b=（
）x-1，c=log
x，且x＞1，则（ ）
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、b＞c＞a |
设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若函数y=f（x）-g（x）在x∈[a，b]上有两个不同的零点，则称f（x）和g（x）在[a，b]上是“关联函数”，区间[a，b]称为“关联区间”．若f（x）=x2-2x-2与g（x）=-x+n在[-1，3]上是“关联函数”，则n的取值范围是（ ）
| A、（-∞，0] | ||
| B、（-∞，4] | ||
C、（-
| ||
D、（-
|
已知向量
=（1-sinθ，1），
=（
，1+sinθ），若
∥
，则锐角θ等于（ ）
| a |
| b |
| 1 |
| 4 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、75° |
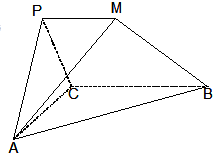在如图所示的多面体PMBCA中，平面PAC⊥平面ABC，△PAC是边长为2的正三角形，PM∥BC，且BC=2PM=4，AB=2