题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象与直线y=b(0<b<A)的三个相邻交点的横坐标分别是2、4、8,则f(x)的单调递增区间为( )
| A、[4k,4k+3](k∈Z) |
| B、[6k,6k+3](k∈Z) |
| C、[4k,4k+5](k∈Z) |
| D、[6k,6k+5](k∈Z) |
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:由题意可得,第一个交点与第三个交点的差是一个周期;第一个交点与第二个交点的中点的横坐标对应的函数值是最大值.从这两个方面考虑可求得参数ω、φ的值,进而利用三角函数的单调性求区间.
解答:
 解:与直线y=b(0<b<A)的三个相邻交点的
解:与直线y=b(0<b<A)的三个相邻交点的
横坐标分别是2,4,8
知函数的周期为T=
=2(
-
),得ω=
,
再由五点法作图可得
•
+φ=
,求得φ=-
,
∴函数f(x)=Asin(
x-
).
令2kπ-
≤
x-
≤2kπ+
,k∈z,
求得x∈[6k,6k+3](k∈Z),
故选:B.
 解:与直线y=b(0<b<A)的三个相邻交点的
解:与直线y=b(0<b<A)的三个相邻交点的横坐标分别是2,4,8
知函数的周期为T=
| 2π |
| ω |
| 4+8 |
| 2 |
| 2+4 |
| 2 |
| π |
| 3 |
再由五点法作图可得
| π |
| 3 |
| 2+4 |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴函数f(x)=Asin(
| π |
| 3 |
| π |
| 2 |
令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
求得x∈[6k,6k+3](k∈Z),
故选:B.
点评:本题主要考查正弦函数的图象性质,充分体现了转化、数形结合思想,属于基础题.

练习册系列答案
相关题目
函数y=
的图象大致是( )
| x2 |
| 2x-1 |
A、 |
B、 |
C、 |
D、 |
若函数,f(x)=x2-3x+4,x∈(1,4]的值域( )
| A、(2,8] | ||
B、[
| ||
| C、[2,+∞) | ||
D、(
|
函数y=ax(a>0且a≠1)在[0,1]上的最大值与最小值的差为
,则a等于( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
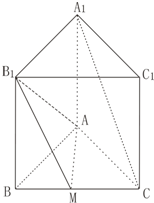 如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.
如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.