题目内容
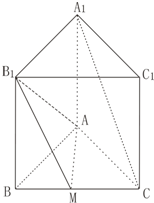 如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.
如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.(1)求二面角M-AB1-B的正切值;
(2)求A1C中点F到面MAB1的距离.
考点:二面角的平面角及求法,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)作MD⊥AB,连接EM,则∠MED为二面角M-AB1-B的平面角,由此能求出二面角M-AB1-B的正切值.
(2)由已知得A1C∥面MAB1,从而F到面MAB1的距离即为C到面MAB1的距离,由VC-MAB=VB-AMC,利用等积法能求出A1C中点F到面MAB1的距离.
(2)由已知得A1C∥面MAB1,从而F到面MAB1的距离即为C到面MAB1的距离,由VC-MAB=VB-AMC,利用等积法能求出A1C中点F到面MAB1的距离.
解答:
解:(1)作MD⊥AB,则DB=
,
DM=
=
,
作DE⊥AB1,DE=
=
=
,
连接EM,则∠MED为二面角M-AB1-B的平面角,
∴tan∠MED=
=
.
(2)连结A1B,交AB1于O,连结MO,
∵M是底面BC边的中点,∴MO∥A1C,
∵MO?面MAB1,A1C 不包含于面MAB1,
∴A1C∥面MAB1,
∴F到面MAB1的距离即为C到面MAB1的距离,设为h,
△AB1M中,MB1=
=
,
AB1=
=
,AM=
,
∴AM2+MB12=AB12,
由VC-MAB=VB-AMC,得
S△ABM•h=
×
×1,
∴h=
.
即A1C中点F到面MAB1的距离为
.
| 1 |
| 4 |

DM=
| BM2-DB2 |
| ||
| 4 |
作DE⊥AB1,DE=
| AD×1 |
| AB |
| ||
|
| 3 | ||
4
|
连接EM,则∠MED为二面角M-AB1-B的平面角,
∴tan∠MED=
| MD |
| ED |
| ||
| 3 |
(2)连结A1B,交AB1于O,连结MO,
∵M是底面BC边的中点,∴MO∥A1C,
∵MO?面MAB1,A1C 不包含于面MAB1,
∴A1C∥面MAB1,
∴F到面MAB1的距离即为C到面MAB1的距离,设为h,
△AB1M中,MB1=
1+(
|
| ||
| 2 |
AB1=
| 1+1 |
| 2 |
| ||
| 2 |
∴AM2+MB12=AB12,
由VC-MAB=VB-AMC,得
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 8 |
∴h=
| ||
| 5 |
即A1C中点F到面MAB1的距离为
| ||
| 5 |
点评:本题考查二面角M-AB1-B的正切值的求法,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
甲、乙、丙三人互相传球,先由甲开始作第一次传球,则5次后球仍回到甲手中的不同传球方式有( )
| A、6 种 | B、8种 |
| C、10种 | D、16种 |
若m、n是正实数,则( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象与直线y=b(0<b<A)的三个相邻交点的横坐标分别是2、4、8,则f(x)的单调递增区间为( )
| A、[4k,4k+3](k∈Z) |
| B、[6k,6k+3](k∈Z) |
| C、[4k,4k+5](k∈Z) |
| D、[6k,6k+5](k∈Z) |