题目内容
在数列{an}中,a1=1,an+1=an+c(c为常数,n∈N*),a1,a2,a5构成公比不等于1的等比数列.记bn=
(n∈N*).
(Ⅰ)求c的值;
(Ⅱ)设{bn}的前n项和为Rn,是否存在正整数k,使得Rk≥2k成立?若存在,找出一个正整数k;若不存在,请说明理由.
| 1 |
| anan+1 |
(Ⅰ)求c的值;
(Ⅱ)设{bn}的前n项和为Rn,是否存在正整数k,使得Rk≥2k成立?若存在,找出一个正整数k;若不存在,请说明理由.
考点:数列的求和,数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(Ⅰ)确定a2=1+c,a5=1+4c,利用a1,a2,a5成等比数列,求c的值;
(Ⅱ)利用裂项法求出{bn}的前n项和为Rn,再计算出是否存在正整数k.
(Ⅱ)利用裂项法求出{bn}的前n项和为Rn,再计算出是否存在正整数k.
解答:
解:(Ⅰ)∵an+1=an+c,a=1,c为常数,
∴{an}是以1为首项,c为公差的等差数列,∴an=1+(n-1)c.…(2分)
∴a2=1+c,a5=1+4c.
又a1,a2,a5成等比数列,∴(1+c)2=1+4c,
解得c=0或c=2.
当c=0时,an+1=an不合题意,舍去.∴c=2.…(4分)
(Ⅱ)由(Ⅰ)知,an=2n-1.…(5分)
∴bn=
=
=
(
-
)…(6分)
∴Rn=b1+b2+…+bn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)=
.…(9分)
假设存在正整数k,使得Rk≥2k,即
≥2k,
∵
=
随k的增大而增大,∴
∈[
,
),而2k≥2
∴不存在正整数k,使得Rk≥2k成立.…(12分)
∴{an}是以1为首项,c为公差的等差数列,∴an=1+(n-1)c.…(2分)
∴a2=1+c,a5=1+4c.
又a1,a2,a5成等比数列,∴(1+c)2=1+4c,
解得c=0或c=2.
当c=0时,an+1=an不合题意,舍去.∴c=2.…(4分)
(Ⅱ)由(Ⅰ)知,an=2n-1.…(5分)
∴bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Rn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
假设存在正整数k,使得Rk≥2k,即
| k |
| 2k+1 |
∵
| k |
| 2k+1 |
| 1 | ||
2+
|
| k |
| 2k+1 |
| 1 |
| 3 |
| 1 |
| 2 |
∴不存在正整数k,使得Rk≥2k成立.…(12分)
点评:此题考查学生灵活运用等比数列的通项公式及前n项和的公式化简求出,会确定一个数列为等比数列,考查数列递推式的求解及相关计算.是一道综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
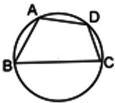 为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.
为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.