题目内容
有10张卡片,其中8张标有数字2,2张标有数字5,从中随机地抽取3张卡片,设3张卡片数字之和为ξ,求E( ξ ) 和D( ξ ).
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:这3张卡片上的数字之和为ξ,这一变量的可能取值为6,9,12.分别求出相应在的概率,由此能求出E( ξ ) 和D( ξ ).
解答:
解:这3张卡片上的数字之和为ξ,这一变量的可能取值为6,9,12.
ξ=6表示取出的3张卡片上标有2,
则P(ξ=6)=
=
.
ξ=9表示取出的3张卡片上两张标有2,一张标有5,
则P(ξ=9)=
=
.
ξ=12表示取出的3张卡片上一张标有2,两张标有5,
则P(ξ=12)=
=
.
∴ξ的分布列为
∴E(ξ)=6×
+9×
+12×
=7.8.
D(ξ)=(6-7.8)2×
+(9-7.8)2×
+(12-7.8)2×
=3.36.
ξ=6表示取出的3张卡片上标有2,
则P(ξ=6)=
| ||
|
| 7 |
| 15 |
ξ=9表示取出的3张卡片上两张标有2,一张标有5,
则P(ξ=9)=
| ||||
|
| 7 |
| 15 |
ξ=12表示取出的3张卡片上一张标有2,两张标有5,
则P(ξ=12)=
| ||||
|
| 1 |
| 15 |
∴ξ的分布列为
| ξ | 6 | 9 | 12 | ||||||
| P |
|
|
|
| 7 |
| 15 |
| 7 |
| 15 |
| 1 |
| 15 |
D(ξ)=(6-7.8)2×
| 7 |
| 15 |
| 7 |
| 15 |
| 1 |
| 15 |
点评:本题考查离散型随机变量的分布列、数学期望和方差的求法,解题时要认真审题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
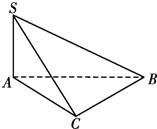 如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2
如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2