题目内容
已知函数f（x）=x3+x2-2x+1．
（1）求f′（x），f′（0），f′（-1）；
（2）求曲线y=f（x）在点（0，1）处的切线方程．
（1）求f′（x），f′（0），f′（-1）；
（2）求曲线y=f（x）在点（0，1）处的切线方程．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：（1）求函数的导数，直接f′（x），f′（0），f′（-1）；
（2）利用导数的几何意义即可求线y=f（x）在点（0，1）处的切线方程．
（2）利用导数的几何意义即可求线y=f（x）在点（0，1）处的切线方程．
解答：
解：（1）∵f（x）=x3+x2-2x+1．
∴函数的导数为f′（x）=3x2+2x-2，
则f′（0）=-2，f′（-1）=3-2-2=-1；
（2）∵f′（0）=-2，
∴曲线y=f（x）在点（0，1）处的切线方程为y-1=2x，
即y=2x+1．
则曲线y=f（x）在点（0，1）处的切线方程为y=2x+1．
∴函数的导数为f′（x）=3x2+2x-2，
则f′（0）=-2，f′（-1）=3-2-2=-1；
（2）∵f′（0）=-2，
∴曲线y=f（x）在点（0，1）处的切线方程为y-1=2x，
即y=2x+1．
则曲线y=f（x）在点（0，1）处的切线方程为y=2x+1．
点评：本题主要考查导数的计算以及导数的几何意义的应用，比较基础．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，|BC|=4，|AC|=3，一曲线E过点A，动点P在曲线E运动，且保持|PC|+|PB|的值不变．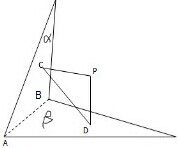
已知P是二面角α-AB-β内一点，PC⊥α，垂足为C，PD⊥β，垂足为D，且PC=3，PD=4，∠CPD=60°，求：