题目内容
甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局,求:
(1)乙取胜的概率;
(2)比赛进行完七局的概率.
(3)记比赛局数为ξ,求ξ的分布列及数学期望Eξ.
(1)乙取胜的概率;
(2)比赛进行完七局的概率.
(3)记比赛局数为ξ,求ξ的分布列及数学期望Eξ.
考点:离散型随机变量及其分布列,n次独立重复试验中恰好发生k次的概率,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)乙取胜有两种情况一是乙连胜四局,二是第三局到第六局中乙胜三局,第七局乙胜,由此能求出乙胜概率.
(2)比赛进行完7局有两种情况:一是甲胜,第3局到第6局中甲胜一局,第7局甲胜,二是乙胜,由此能求出比赛进行完七局的概率.
(3)由题意得ξ=4,5,6,7,分别求出相应的概率,由此能求出ξ的分布列及数学期望Eξ.
(2)比赛进行完7局有两种情况:一是甲胜,第3局到第6局中甲胜一局,第7局甲胜,二是乙胜,由此能求出比赛进行完七局的概率.
(3)由题意得ξ=4,5,6,7,分别求出相应的概率,由此能求出ξ的分布列及数学期望Eξ.
解答:
解:(1)乙取胜有两种情况
一是乙连胜四局,其概率P1=(
)4=
二是第三局到第六局中乙胜三局,第七局乙胜,
其概率P2=
(
)3(1-
)•
=
,
所以乙胜概率为P1+P2=
.
(2)比赛进行完7局有两种情况:
一是甲胜,第3局到第6局中甲胜一局,第7局甲胜,
其概率p3=
•
(1-
)3•
=
.
二是乙胜,同(1)中第二种情况,
P4=P2=
,
∴比赛进行完七局的概率为:P3+P4=
.
(3)由题意得ξ=4,5,6,7,
P(ξ=4)=(
)2=
,
P(ξ=5)=
(
)2•
=
,
P(ξ=6)=(
)4+
(
)3•
=
,
P(ξ=7)=
,
所以ξ的分布列为
Eξ=(4+5+6+7)×
=
.
一是乙连胜四局,其概率P1=(
| 1 |
| 2 |
| 1 |
| 16 |
二是第三局到第六局中乙胜三局,第七局乙胜,
其概率P2=
| C | 3 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
所以乙胜概率为P1+P2=
| 3 |
| 16 |
(2)比赛进行完7局有两种情况:
一是甲胜,第3局到第6局中甲胜一局,第7局甲胜,
其概率p3=
| C | 1 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
二是乙胜,同(1)中第二种情况,
P4=P2=
| 1 |
| 8 |
∴比赛进行完七局的概率为:P3+P4=
| 1 |
| 4 |
(3)由题意得ξ=4,5,6,7,
P(ξ=4)=(
| 1 |
| 2 |
| 1 |
| 4 |
P(ξ=5)=
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
P(ξ=6)=(
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
P(ξ=7)=
| 1 |
| 4 |
所以ξ的分布列为
| ξ | 4 | 5 | 6 | 7 | ||||||||
| P |
|
|
|
|
| 1 |
| 4 |
| 11 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
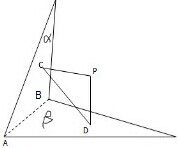 已知P是二面角α-AB-β内一点,PC⊥α,垂足为C,PD⊥β,垂足为D,且PC=3,PD=4,∠CPD=60°,求:
已知P是二面角α-AB-β内一点,PC⊥α,垂足为C,PD⊥β,垂足为D,且PC=3,PD=4,∠CPD=60°,求: