题目内容
在极坐标系下，O是极点，已知A（3，
），B（4，-
），则△AOB的面积为 ．
| π |
| 3 |
| π |
| 6 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：由A（3，
），B（4，-
），可得∠AOB=
+
=
．即可得出．
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
解答：
解：∵A（3，
），B（4，-
），
∴∠AOB=
+
=
．
∴△AOB的面积S=
×3×4=6．
故答案为：6．
| π |
| 3 |
| π |
| 6 |
∴∠AOB=
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴△AOB的面积S=
| 1 |
| 2 |
故答案为：6．
点评：本题考查了极坐标的意义、三角形的面积计算公式，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
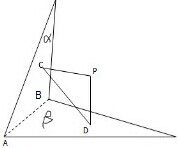已知P是二面角α-AB-β内一点，PC⊥α，垂足为C，PD⊥β，垂足为D，且PC=3，PD=4，∠CPD=60°，求：