题目内容
（1）已知z=1+i，设w=z2+3
-4，求w．
（2）已知复数z满足条件|z-i|=|3+4i|，求复数z在复平面上对应的点的轨迹方程．
. |
| z |
（2）已知复数z满足条件|z-i|=|3+4i|，求复数z在复平面上对应的点的轨迹方程．
考点：轨迹方程,复数代数形式的乘除运算
专题：计算题,圆锥曲线的定义、性质与方程
分析：（1）利用复数的运算，可求w．
（2）利用复数模的几何意义，求复数z在复平面上对应的点的轨迹方程．
（2）利用复数模的几何意义，求复数z在复平面上对应的点的轨迹方程．
解答：
解：（1）∵z=1+i，
∴w=z2+3
-4=2i+3（1-i）-4=-1-i；
（2）设z=（x，y），则
∵复数z满足条件|z-i|=|3+4i|，
∴x2+（y-1）2=16．
∴w=z2+3
. |
| z |
（2）设z=（x，y），则
∵复数z满足条件|z-i|=|3+4i|，
∴x2+（y-1）2=16．
点评：本题考查求复数z在复平面上对应的点的轨迹方程．考查学生的计算能力，比较基础．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，|BC|=4，|AC|=3，一曲线E过点A，动点P在曲线E运动，且保持|PC|+|PB|的值不变．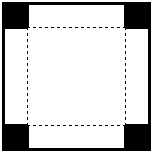
如图，一边长为48cm的正方形铁皮，在它的四角上切去相等的小正方形，再把它的边沿虚线折起，做成一个无盖的方底箱子，箱底的边长是多少时，箱子的容积最大？最大容积是多少？