题目内容
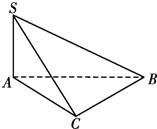 如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2
如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2| 3 |
(1)求SC与平面ABC所成的角;
(2)求SC与平面SAB所成的角.
考点:直线与平面所成的角
专题:空间位置关系与距离
分析:(1)首先要求SC与平面ABC所成的角,可以通过线面的垂直进行转化,求∠SCA的大小可以通过解直角三角形知识求解.
(2)要求SC与平面SAB所成的角,可以通过作垂线,转化成求∠CSD的大小,然后通过解直角三角形知识来求解.
(2)要求SC与平面SAB所成的角,可以通过作垂线,转化成求∠CSD的大小,然后通过解直角三角形知识来求解.
解答:
解:(1)∵∠ACB=90°,AC=1,∠ABC=30°,∴AB=2.
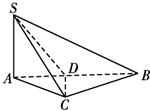
∵SA⊥面ABC,
∴∠SCA就是SC与平面ABC所成的角.
在Rt△SAC中,AC=1,SA=
=2
.
∴tan∠SCA=
=2
.
∴∠SCA=arctan 2
.
即SC与平面ABC所成的角为arctan 2
.
(2)作CD⊥AB于D,
∵SA⊥面ABC,
∴SA⊥CD,
∴CD⊥面SAB,
∴∠CSD就是SC与平面SAB所成的角.
在Rt△CDS中,CD=BC•sin 30°=
,SC=
=3,
∴sin∠CSD=
=
,
∴∠CSD=arcsin
,
即SC与平面SAB所成的角为arcsin
.
故答案为:
(1)SC与平面ABC所成的角为arctan 2
.
(2)SC与平面SAB所成的角为arcsin
.

∵SA⊥面ABC,
∴∠SCA就是SC与平面ABC所成的角.
在Rt△SAC中,AC=1,SA=
| SB2-AB2 |
| 2 |
∴tan∠SCA=
| SA |
| AC |
| 2 |
∴∠SCA=arctan 2
| 2 |
即SC与平面ABC所成的角为arctan 2
| 2 |
(2)作CD⊥AB于D,
∵SA⊥面ABC,
∴SA⊥CD,
∴CD⊥面SAB,
∴∠CSD就是SC与平面SAB所成的角.
在Rt△CDS中,CD=BC•sin 30°=
| ||
| 2 |
| SA2+AC2 |
∴sin∠CSD=
| CD |
| SC |
| ||
| 6 |
∴∠CSD=arcsin
| ||
| 6 |
即SC与平面SAB所成的角为arcsin
| ||
| 6 |
故答案为:
(1)SC与平面ABC所成的角为arctan 2
| 2 |
(2)SC与平面SAB所成的角为arcsin
| ||
| 6 |
点评:本题考查的知识点:线面垂直的性质定理,线面夹角的转化,解直角三角形,三角函数的定义.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
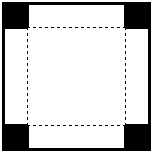 如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?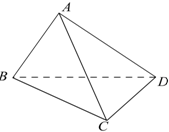 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.