题目内容
今年暑假期间有一个自驾游车队,组织车友前往青海游玩.该车队是由31辆车身长都约为5m(以5m计算)的同一车型组成的,行程中经过一个长为2725m的隧道(通过该隧道的速度不能超过20m/s),匀速通过该隧道,设车队速度为xm/s,根据安全和车流的需要,当0<x≤12时,相邻两车之间保持20m的距离,当12<x≤20时,相邻两车之间保持(
x2+
x)m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为
y(s).
(Ⅰ)将y表示成x的函数;
(Ⅱ)求该车队通过隧道时间y的最小值及此时车队的速度.
| 1 |
| 6 |
| 1 |
| 3 |
y(s).
(Ⅰ)将y表示成x的函数;
(Ⅱ)求该车队通过隧道时间y的最小值及此时车队的速度.
考点:函数模型的选择与应用,函数的最值及其几何意义
专题:应用题,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)利用当0<x≤12时,相邻两车之间保持20m的距离;当12<x≤25时,相邻两车之间保持(
x2+
x)m的距离,可得分段函数;
(Ⅱ)分段求出函数的最小值,即可得到分段函数的最小值.
| 1 |
| 6 |
| 1 |
| 3 |
(Ⅱ)分段求出函数的最小值,即可得到分段函数的最小值.
解答:
解:(Ⅰ)当0<x≤12时,y=
=
; …2分
当12<x≤20时,y=
=
=5x+
+10;…4分
∴所求函数解析式为y=
. …6分
(Ⅱ)当0<x≤12时,由于函数单调递减,所以在x=12m/s时,ymin=
=290(s);…8分
当12<x≤20时,y=5x+
+10≥2
+10=250(s),
其中等号当且仅当5x=
即x=24时成立.
但24∉(12,20],且当12<x≤20时,y′=5-
=
<0,
所以函数在(12,20]上也单调递减,从而,当x=20时,ymin=254(s) …12分
因290>254,所以ymin=254(s).
答:当车队速度为20m/s时,车队通过隧道时间最小,最小时间为254s. …13分.
| 2725+5×31+20×(31-1) |
| x |
| 3480 |
| x |
当12<x≤20时,y=
2725+5×31+(
| ||||
| x |
| 5x2+10x+2880 |
| x |
| 2880 |
| x |
∴所求函数解析式为y=
|
(Ⅱ)当0<x≤12时,由于函数单调递减,所以在x=12m/s时,ymin=
| 3490 |
| 12 |
当12<x≤20时,y=5x+
| 2880 |
| x |
5x•
|
其中等号当且仅当5x=
| 2880 |
| x |
但24∉(12,20],且当12<x≤20时,y′=5-
| 2880 |
| x2 |
| 5x2-2880 |
| x2 |
所以函数在(12,20]上也单调递减,从而,当x=20时,ymin=254(s) …12分
因290>254,所以ymin=254(s).
答:当车队速度为20m/s时,车队通过隧道时间最小,最小时间为254s. …13分.
点评:本题考查分段函数模型的构建,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,
2+
•
<0,则△ABC为( )
| AB |
| AB |
| BC |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角或钝角三角形 |
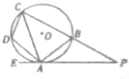 如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明:
如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明: