题目内容
2012年伦敦奥运会伦敦站的火炬传递中邀请了5位奥运冠军和3位歌手参加传递，
（Ⅰ） 若3位歌手互不相邻，求伦敦站的不同传递方案的种数．（直接用数字作答）
（Ⅱ）在这8位参加传递的人中选3人参加一项奥运宣传活动，用X表示参加此次宣传活动的歌手的人数．
①列出X的所有可能的取值结果；
②求随机变量X的分布列；
③求参加此次活动的人中歌手至少有2名的概率．
（Ⅰ） 若3位歌手互不相邻，求伦敦站的不同传递方案的种数．（直接用数字作答）
（Ⅱ）在这8位参加传递的人中选3人参加一项奥运宣传活动，用X表示参加此次宣传活动的歌手的人数．
①列出X的所有可能的取值结果；
②求随机变量X的分布列；
③求参加此次活动的人中歌手至少有2名的概率．
考点：离散型随机变量及其分布列,离散型随机变量的期望与方差
专题：概率与统计
分析：（1）由3位歌手互不相邻，利用插空法能求出伦敦站的不同传递方案的种数．
（2）X的所有可能的取值结果为：0，1，2，3，分别求出相应的概率，由此能求出随机变量X的分布列和概率．
（2）X的所有可能的取值结果为：0，1，2，3，分别求出相应的概率，由此能求出随机变量X的分布列和概率．
解答：
解：（1）∵3位歌手互不相邻，
∴伦敦站的不同传递方案的种数为：
•
=14400．…（2分）
（2）①X的所有可能的取值结果为：0，1，2，3．…（3分）
②P(X=0)=
=
，P(X=1)=
=
，P(X=2)=
=
，P(X=0)=
=
所以随机变量X的分布列为：
…（10分）
③参加此次活动的人中歌手至少有2名的概率为：P(X≥2)=P(X=2)+P(X=3)=
+
=
…（13分）..
∴伦敦站的不同传递方案的种数为：
| A | 5 5 |
| A | 3 6 |
（2）①X的所有可能的取值结果为：0，1，2，3．…（3分）
②P(X=0)=
| ||||
|
| 5 |
| 28 |
| ||||
|
| 15 |
| 28 |
| ||||
|
| 15 |
| 56 |
| ||||
|
| 1 |
| 56 |
所以随机变量X的分布列为：
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
③参加此次活动的人中歌手至少有2名的概率为：P(X≥2)=P(X=2)+P(X=3)=
| 15 |
| 56 |
| 1 |
| 56 |
| 2 |
| 7 |
点评：本题考查的不同传递方案的种数的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，在历年高考中都是必考题型之一．
练习册系列答案
相关题目
如图执行下面的流程图，那么输出的S等于（ ）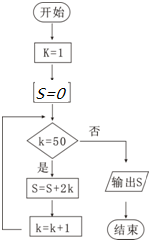
| A、2450 | B、2500 |
| C、2550 | D、2652 |
双曲线
-
=1（a＞0，b＞0）的左右焦点分别为F1，F2，过焦点F2与x轴垂直的直线与双曲线交于P，Q两点，若△PF1Q是等边三角形，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
C、
| ||
D、2
|
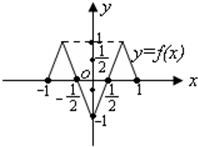已知函数y=f（x）的定义域和值域都是[-1，1]（其图象如图所示），函数g（x）=sinx，x∈[-π，π]．定义：当f（x1）=0（x1∈[-1，1]）且g（x2）=x1（x2∈[-π，π]）时，称x2是方程f（g（x））=0的一个实数根．则方程f（g（x））=0的所有不同实数根的个数是点P是以F为焦点的抛物线y2=4x上的动点，则以P为圆心，以线段PF的长为半径的圆与直线x=-1的位置关系是（ ）
| A、相切 | B、相交 |
| C、相离 | D、随点P的位置变化而变化 |