题目内容
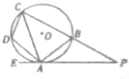 如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明:
如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明:(1)AD=AB;
(2)DA2=DC•BP.
考点:与圆有关的比例线段
专题:立体几何
分析:(1)连结BD,由弦切角定理得∠EAD=∠ABD=∠PCA,由此能证明AD=AB.
(2)由已知得∠ADC=∠ABP,∠PAB=∠ACD,从而△ACD∽△APB,由此能证明DA2=DC•BP.
(2)由已知得∠ADC=∠ABP,∠PAB=∠ACD,从而△ACD∽△APB,由此能证明DA2=DC•BP.
解答:
证明:(1)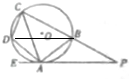 连结BD,
连结BD,
∵四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,∠EAD=∠PCA,
∴∠EAD=∠ABD=∠PCA,
∴AD=AB.
(2)∵四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,∠EAD=∠PCA,
∴∠ADC=∠ABP,∠PAB=∠ACD,
∴△ACD∽△APB,
∴
=
,又AD=AB,
∴DA2=DC•BP.
 连结BD,
连结BD,∵四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,∠EAD=∠PCA,
∴∠EAD=∠ABD=∠PCA,
∴AD=AB.
(2)∵四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,∠EAD=∠PCA,
∴∠ADC=∠ABP,∠PAB=∠ACD,
∴△ACD∽△APB,
∴
| AD |
| BP |
| CD |
| AB |
∴DA2=DC•BP.
点评:本题考查线段长相等的证明,考查DA2=DC•BP的证明,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
相关题目
点P是以F为焦点的抛物线y2=4x上的动点,则以P为圆心,以线段PF的长为半径的圆与直线x=-1的位置关系是( )
| A、相切 | B、相交 |
| C、相离 | D、随点P的位置变化而变化 |
设直线过点(0,a),其斜率为1,且与圆x2+y2=4相切,则a的值为( )
| A、±4 | ||
B、±2
| ||
| C、4x+2y=5 | ||
| D、4x-2y=5 |
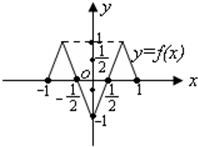 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是