题目内容
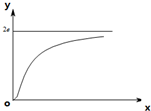函数y=ae•e| b |
| x |
| A、a=2，b=-1 |
| B、a=1，b=-1 |
| C、a=1，b=1 |
| D、a=2，b=1 |
考点：函数的图象
专题：数形结合,函数的性质及应用
分析：利用函数图象的单调性，值域以及函数值的符号，进行推理判断即可．
解答：
解：由函数图象可知，当x＞0时，函数y＞0，所以可知a＞0．
因为函数的值域为（0，2e），所以可知a=2．排除B，C．
设t=
，则y=ae•et，
因为函数y=ae•et单调递增，由图象可知函数y=ae•e
在（0，+∞）上单调递增，
所以根据复合函数“同增异减”的关系可知，函数t=
为增函数，所以b＜0，排除D．
故只有A有可能．
故选A．
因为函数的值域为（0，2e），所以可知a=2．排除B，C．
设t=
| b |
| x |
因为函数y=ae•et单调递增，由图象可知函数y=ae•e
| b |
| x |
所以根据复合函数“同增异减”的关系可知，函数t=
| b |
| x |
故只有A有可能．
故选A．
点评：本题主要考查函数图象的识别和判断，充分利用函数图象的单调性，取值范围，以及最值的性质是判断函数图象的基本方法．
练习册系列答案
相关题目
设集合A={(x，y)|xy(
+
)+|x+y-1|≤1}，B={(x，y)|x2+y2≤1}，则在同一直角坐标平面内，A∩B所形成区域的面积为（ ）
| 1 |
| |x| |
| 1 |
| |y| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|