题目内容
已知函数f(x)=
(x∈R),点P1(x1,y1),P2(x2,y2)是函数f(x)图象上的两个点,且线段P1P2的中点P的横坐标为
.
(Ⅰ)求证:点P的纵坐标是定值;
(Ⅱ)若数列{an}的通项公式为an=f(
)(m∈N,n=1,2,…,m),求数列{an}的前m项的和Sm.
| 1 |
| 4x+2 |
| 1 |
| 2 |
(Ⅰ)求证:点P的纵坐标是定值;
(Ⅱ)若数列{an}的通项公式为an=f(
| n |
| m |
考点:数列的求和,有理数指数幂的化简求值
专题:综合题
分析:(Ⅰ)由题可知:x1+x2=2×
=1,由y1+y2=f(x1)+f(x2)=
+
化简整理可得y1+y2=
,从而可证点P的纵坐标是定值;
(Ⅱ)由(Ⅰ)可知:对任意自然数m,n,f(
)+f(
)=
恒成立,Sm=f(
)+f(
)+…+f(
)+f(
)+f(
),利用倒序相加法及可求得答案.
| 1 |
| 2 |
| 1 |
| 4x1+2 |
| 1 |
| 4x2+2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)可知:对任意自然数m,n,f(
| n |
| m |
| m-n |
| m |
| 1 |
| 2 |
| 1 |
| m |
| 2 |
| m |
| m-2 |
| m |
| m-1 |
| m |
| m |
| m |
解答:
解:(Ⅰ)由题可知:x1+x2=2×
=1,所以,y1+y2=f(x1)+f(x2)=
+
=
=
=
=
点P的纵坐标yP=
=
是定值,问题得证.
(Ⅱ)由(Ⅰ)可知:对任意自然数m,n,f(
)+f(
)=
恒成立.
由于Sm=f(
)+f(
)+…+f(
)+f(
)+f(
),故可考虑利用倒写求和的方法.
即由于:Sm=f(
)+f(
)+…+f(
)+f(
)+f(
)
=f(
)+f(
)+f(
)+…+f(
)+f(
),
所以,2Sm=[f(
)+f(
)]+[f(
)+f(
)]+…+[f(
)+f(
)]+2f(
)
=
(m-1)+2f(1)=
(3m-1).
所以,Sm=
(3m-1).
| 1 |
| 2 |
| 1 |
| 4x1+2 |
| 1 |
| 4x2+2 |
| 4x1+4x2+4 |
| (4x1+2)(4x2+2) |
|
|
| 1 |
| 2 |
点P的纵坐标yP=
| y1+y2 |
| 2 |
| 1 |
| 4 |
(Ⅱ)由(Ⅰ)可知:对任意自然数m,n,f(
| n |
| m |
| m-n |
| m |
| 1 |
| 2 |
由于Sm=f(
| 1 |
| m |
| 2 |
| m |
| m-2 |
| m |
| m-1 |
| m |
| m |
| m |
即由于:Sm=f(
| 1 |
| m |
| 2 |
| m |
| m-2 |
| m |
| m-1 |
| m |
| m |
| m |
=f(
| m |
| m |
| m-1 |
| m |
| m-2 |
| m |
| 2 |
| m |
| 1 |
| m |
所以,2Sm=[f(
| 1 |
| m |
| m-1 |
| m |
| 2 |
| m |
| m-2 |
| m |
| m-1 |
| m |
| 1 |
| m |
| m |
| m |
=
| 1 |
| 2 |
| 1 |
| 6 |
所以,Sm=
| 1 |
| 12 |
点评:本题考查数列的求和,着重考查有理数指数幂的化简求值,突出倒序相加法求和的考查,考查化简与运算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( )


| A、甲=乙=丙 |
| B、甲<乙<丙 |
| C、乙<丙<甲 |
| D、丙<乙<甲 |
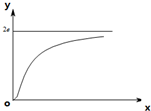 函数y=ae•e
函数y=ae•e| b |
| x |
| A、a=2,b=-1 |
| B、a=1,b=-1 |
| C、a=1,b=1 |
| D、a=2,b=1 |
已知
=(sina-cosa,2007),
=(sina+cosa,1),且
∥
,则tan2a-
=( )
| a |
| b |
| a |
| b |
| 1 |
| cos2a |
| A、-2007 | ||
B、-
| ||
| C、2007 | ||
D、
|