题目内容
设函f(x)=xekx(k≠0)
(1)求曲y=f(x)在(0,f(0))出的切线方程.
(2)求函f(x)的单调区间.
(1)求曲y=f(x)在(0,f(0))出的切线方程.
(2)求函f(x)的单调区间.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
(2)先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间即可;
(2)先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间即可;
解答:
解:(1)f′(x)=(1+kx)ekx,f′(0)=1,f(0)=0,
曲线y=f(x)在点(0,f(0))处的切线方程为y=x;
(2)由f′(x)=(1+kx)ekx=0,得x=-
(k≠0),
①若k>0,则当x∈(-∞,-
)时,
f′(x)<0,函数f(x)单调递减,
当x∈(-
,+∞)时,f′(x)>0,
函数f(x)单调递增,
②若k<0,则当x∈(-∞,-
)时,
f′(x)>0,函数f(x)单调递增,
当x∈(-
,+∞)时,
f′(x)<0,函数f(x)单调递减.
综上可知,当k>0时,函数f(x)单调递增区间为(-
,+∞),函数f(x)单调递减区间为(-∞,-
);
当k<0时,函数f(x)单调递增区间为(-∞,-
),函数f(x)单调递减区间为(-
,+∞).
曲线y=f(x)在点(0,f(0))处的切线方程为y=x;
(2)由f′(x)=(1+kx)ekx=0,得x=-
| 1 |
| k |
①若k>0,则当x∈(-∞,-
| 1 |
| k |
f′(x)<0,函数f(x)单调递减,
当x∈(-
| 1 |
| k |
函数f(x)单调递增,
②若k<0,则当x∈(-∞,-
| 1 |
| k |
f′(x)>0,函数f(x)单调递增,
当x∈(-
| 1 |
| k |
f′(x)<0,函数f(x)单调递减.
综上可知,当k>0时,函数f(x)单调递增区间为(-
| 1 |
| k |
| 1 |
| k |
当k<0时,函数f(x)单调递增区间为(-∞,-
| 1 |
| k |
| 1 |
| k |
点评:本小题主要考查直线的斜率、利用导数研究函数的单调性、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力以及分类讨论思想.

练习册系列答案
相关题目
如果二次方程x2-px-q=0(p,q∈N*) 的正根小于3,那么这样的二次方程有( )
| A、5个 | B、6个 | C、7个 | D、8个 |
图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).图②中E为AB的中点,图③中AJ>JB.判断三人行进路线长度的大小关系为( )


| A、甲=乙=丙 |
| B、甲<乙<丙 |
| C、乙<丙<甲 |
| D、丙<乙<甲 |
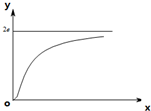 函数y=ae•e
函数y=ae•e| b |
| x |
| A、a=2,b=-1 |
| B、a=1,b=-1 |
| C、a=1,b=1 |
| D、a=2,b=1 |