题目内容
已知A={x|x2+5x-6=0},B={x|ax-1=0},若B⊆A,则实数a的值为 .
考点:集合的包含关系判断及应用
专题:计算题
分析:先化简A,再根据B⊆A分情况对参数的取值分当a=0时和当a≠0时两种情况,进行讨论,即可求出参数a的取值集合.
解答:
解:当a=0时,集合B={x|ax-1=0}=∅,满足B⊆A,
当a≠0时,集合B={x|ax-1=0}={
},
∵集合A={x|x2+5x-6=0}={1,-6},B⊆A,
∴
=1,或
=-6
∴a=1,或a=-6
综上所述a的值是0,1,-
故答案为:0,1,-
当a≠0时,集合B={x|ax-1=0}={
| 1 |
| a |
∵集合A={x|x2+5x-6=0}={1,-6},B⊆A,
∴
| 1 |
| a |
| 1 |
| a |
∴a=1,或a=-6
综上所述a的值是0,1,-
| 1 |
| 6 |
故答案为:0,1,-
| 1 |
| 6 |
点评:本题考查集合关系中的参数取值问题,解题的关键是根据包含关系的定义对集合Q的情况进行正确分类,本题求解中有一易错点,就是忘记讨论Q是空集的情况,分类讨论时一定注意不要漏掉情况.

练习册系列答案
相关题目
若关于x的一元二次方程x2-(m-1)x-m=0有两个不相等的实数根,则m的取值集合是( )
| A、R |
| B、{m|m≠1} |
| C、{m|m≠-1} |
| D、{m|m>-1} |
如果二次方程x2-px-q=0(p,q∈N*) 的正根小于3,那么这样的二次方程有( )
| A、5个 | B、6个 | C、7个 | D、8个 |
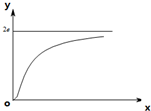 函数y=ae•e
函数y=ae•e| b |
| x |
| A、a=2,b=-1 |
| B、a=1,b=-1 |
| C、a=1,b=1 |
| D、a=2,b=1 |
sin45°的值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |