题目内容
直线x+y+b=0平分圆x2+y2+2x=0的面积，则b= ．
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：根据直线平分圆的面积，得到直线过圆心，将圆心坐标代入直线方程即可求出b的值．
解答：
解：将圆方程变形得：（x+1）2+y2=1，即圆心（-1，0），半径r=1，
∵直线x+y+b=0平分圆x2+y2+2x=0的面积，
∴直线x+y+b=0过圆心（-1，0），
将x=-1，y=0代入直线方程得：-1+0+b=0，
解得：b=1．
故答案为：1
∵直线x+y+b=0平分圆x2+y2+2x=0的面积，
∴直线x+y+b=0过圆心（-1，0），
将x=-1，y=0代入直线方程得：-1+0+b=0，
解得：b=1．
故答案为：1
点评：此题考查了直线与圆的位置关系，根据题意得出直线过圆心是解本题的关键．
练习册系列答案
相关题目
已知圆C1：x2+y2-2x=0，圆C2：x2+y2-2y-4=0则两圆的位置关系是（ ）
| A、外切 | B、相交 | C、内切 | D、内含 |
若关于x的一元二次方程x2-（m-1）x-m=0有两个不相等的实数根，则m的取值集合是（ ）
| A、R |
| B、{m|m≠1} |
| C、{m|m≠-1} |
| D、{m|m＞-1} |
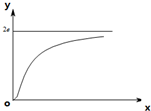函数y=ae•e| b |
| x |
| A、a=2，b=-1 |
| B、a=1，b=-1 |
| C、a=1，b=1 |
| D、a=2，b=1 |