题目内容
已知在极坐标系下，圆C的方程为ρ=4cosθ，直线l的方程为3ρcosθ-4ρsinθ-1=0，则直线l截圆C所得的弦长为 ．
考点：简单曲线的极坐标方程
专题：计算题
分析：化圆与直线的极坐标方程为直角坐标方程，求出圆心到直线的距离，利用勾股定理求出半弦长，则直线l截圆C所得的弦长可求．
解答：
解：由ρ=4cosθ，得ρ2=4ρcosθ，即x2-4x+y2=0．
整理得，（x-2）2+y2=4，所以圆C是以（2，0）为圆心，以2为半径的圆．
由3ρcosθ-4ρsinθ-1=0，得3x-4y-1=0．
所以圆心（2，0）到直线3x-4y-1=0的距离为d=
=1．
则直线l被圆C所截得的半弦长为
=
．
所以直线l截圆C所得的弦长为2
．
故答案为2
．
整理得，（x-2）2+y2=4，所以圆C是以（2，0）为圆心，以2为半径的圆．
由3ρcosθ-4ρsinθ-1=0，得3x-4y-1=0．
所以圆心（2，0）到直线3x-4y-1=0的距离为d=
| |3×2-4×0-1| | ||
|
则直线l被圆C所截得的半弦长为
| 22-12 |
| 3 |
所以直线l截圆C所得的弦长为2
| 3 |
故答案为2
| 3 |
点评：本题考查了简单曲线的极坐标方程，训练了点到直线的距离公式，是基础的运算题．
练习册系列答案
相关题目
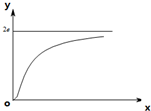函数y=ae•e| b |
| x |
| A、a=2，b=-1 |
| B、a=1，b=-1 |
| C、a=1，b=1 |
| D、a=2，b=1 |
设等比数列{an}的首项a1和公比q都是正数，且q≠1，则下列判断正确的是（ ）
| A、a1+a8＞a4+a5 |
| B、a1+a8＜a4+a5 |
| C、a1+a8=a4+a5 |
| D、a1+a8与a4+a5的大小关系不能确定 |