题目内容
若a＞0，b＞0则
+
（填上适当的等号或不等号）．
| a |
| b |
| a+b |
考点：不等式比较大小
专题：综合题
分析：把要比较的两个数平方后作差判断符号，因为两个数都大于0，然后得到要比较的两个数的大小．
解答：
解：∵a＞0，b＞0，
∴(
+
)2-(
)2=a+b+2
-a-b=2
＞0．
∴(
+
)2＞(
)2．
则
+
＞
．
故答案为：＞．
∴(
| a |
| b |
| a+b |
| ab |
| ab |
∴(
| a |
| b |
| a+b |
则
| a |
| b |
| a+b |
故答案为：＞．
点评：本题考查了不等式的大小比较，考查了不等式的性质，是基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知圆C1：x2+y2-2x=0，圆C2：x2+y2-2y-4=0则两圆的位置关系是（ ）
| A、外切 | B、相交 | C、内切 | D、内含 |
图①、图②、图③分别表示甲、乙、丙三人由A地到B地的路线图（箭头表示行进的方向）．图②中E为AB的中点，图③中AJ＞JB．判断三人行进路线长度的大小关系为（ ）
| A、甲=乙=丙 |
| B、甲＜乙＜丙 |
| C、乙＜丙＜甲 |
| D、丙＜乙＜甲 |
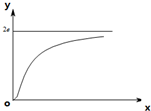函数y=ae•e| b |
| x |
| A、a=2，b=-1 |
| B、a=1，b=-1 |
| C、a=1，b=1 |
| D、a=2，b=1 |
已知
=（sina-cosa，2007），
=（sina+cosa，1），且
∥
，则tan2a-
=（ ）
| a |
| b |
| a |
| b |
| 1 |
| cos2a |
| A、-2007 | ||
B、-
| ||
| C、2007 | ||
D、
|
设等比数列{an}的首项a1和公比q都是正数，且q≠1，则下列判断正确的是（ ）
| A、a1+a8＞a4+a5 |
| B、a1+a8＜a4+a5 |
| C、a1+a8=a4+a5 |
| D、a1+a8与a4+a5的大小关系不能确定 |