题目内容
已知函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
.
(1)确定函数f(x)的解析式;
(2)用定义证明f(x)在(-1,1)上是增函数;
(3)解不等式f(t-1)+f(2t)<0.
| ax+b |
| 1+x2 |
| 1 |
| 3 |
| 3 |
| 5 |
(1)确定函数f(x)的解析式;
(2)用定义证明f(x)在(-1,1)上是增函数;
(3)解不等式f(t-1)+f(2t)<0.
考点:函数单调性的判断与证明,其他不等式的解法
专题:函数的性质及应用
分析:(1)由题意得方程组,解出a,b的值,从而求出函数的表达式;
(2)证明:设?-1<x1<x2<1,得出f(x1)<f(x2),从而得出f(x)的单调性;
(3)由f(t-1)+f(2t)<0,得出f(t-1)<-f(2t)=f(-2t),结合函数的单调性得出-1<t-1<-2t<1,解出即可.
(2)证明:设?-1<x1<x2<1,得出f(x1)<f(x2),从而得出f(x)的单调性;
(3)由f(t-1)+f(2t)<0,得出f(t-1)<-f(2t)=f(-2t),结合函数的单调性得出-1<t-1<-2t<1,解出即可.
解答:
(1)解:由题意得:
,解得:
;
∴f(x)=
;
(2)证明:设?-1<x1<x2<1,
则f(x1)-f(x2)=
,
∵-1<x1<x2<1,x1-x2<0,1-x1x2>0,从而f(x1)-f(x2)<0,
即f(x1)<f(x2),∴f(x)在(-1,1)上递增;
(3)解:∵f(t-1)+f(2t)<0,
∴f(t-1)<-f(2t)=f(-2t),
∵函数f(x)在(-1,1)上递增,
∴-1<t-1<-2t<1,解得:0<t<
,
∴原不等式的解集为:(0,
).
|
|
∴f(x)=
| 2x |
| 1+x2 |
(2)证明:设?-1<x1<x2<1,
则f(x1)-f(x2)=
| 2(x1-x2)(1-x1x2) |
| (1+x12)(1+x22) |
∵-1<x1<x2<1,x1-x2<0,1-x1x2>0,从而f(x1)-f(x2)<0,
即f(x1)<f(x2),∴f(x)在(-1,1)上递增;
(3)解:∵f(t-1)+f(2t)<0,
∴f(t-1)<-f(2t)=f(-2t),
∵函数f(x)在(-1,1)上递增,
∴-1<t-1<-2t<1,解得:0<t<
| 1 |
| 3 |
∴原不等式的解集为:(0,
| 1 |
| 3 |
点评:本题考查了函数的单调性问题,求函数的解析式问题,考查函数的奇偶性,是一道中档题.

练习册系列答案
相关题目
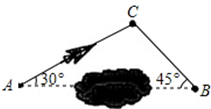 一架飞机从马来西亚吉隆坡飞往中国北京,两地相距4500km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到途中,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程4500km远了多少?(参考数据:
一架飞机从马来西亚吉隆坡飞往中国北京,两地相距4500km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到途中,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程4500km远了多少?(参考数据: