题目内容
 如图,半径为30cm的圆形(O为圆心)铁皮上截取一块矩形材料OABC,其中点B在圆弧上,点A,C在两半径上,现将此矩形材料卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设OB与矩形材料的边OA的夹角为θ,圆柱的体积为Vcm3.
如图,半径为30cm的圆形(O为圆心)铁皮上截取一块矩形材料OABC,其中点B在圆弧上,点A,C在两半径上,现将此矩形材料卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设OB与矩形材料的边OA的夹角为θ,圆柱的体积为Vcm3.(Ⅰ)求V关于θ的函数关系式,并写出定义域;
(Ⅱ)求圆柱形罐子体积V的最大值.
考点:函数模型的选择与应用
专题:导数的综合应用
分析:(Ⅰ)由已知条件寻找数量间的等式关系,由此能求出圆柱的体积V关于θ的函数关系式.
(Ⅱ)令t=sinθ,t∈(0,1),cos2θ=1-t2,f(t)=
,t∈(0,1),f′(x)=
,由此利用导数性质能求出体积的最大值.
(Ⅱ)令t=sinθ,t∈(0,1),cos2θ=1-t2,f(t)=
| 6750(t-t3) |
| π |
| 6750(1-3t2) |
| π |
解答:
解:(Ⅰ)∵半径为30cm的圆形(O为圆心)铁皮上截取一块矩形材料OABC,
设OB与矩形材料的边OA的夹角为θ,圆柱的体积为V cm3.
∴V(θ)=
=
,0<θ<
.
(Ⅱ)令t=sinθ,t∈(0,1),cos2θ=1-t2,
∴f(t)=
,t∈(0,1),
∴f′(x)=
,
由f′(t)=0,得t=
,或t=-
(舍),
由f′(t)>0,得0<t<
;由f′(t)<0,得
<t<1.
∴f(x)在(0,
)上单调递增,在(
,1)上单调递减,
即当t=
时,体积V取得最大值Vmax=
cm3.
设OB与矩形材料的边OA的夹角为θ,圆柱的体积为V cm3.
∴V(θ)=
| 303cos2θsinθ |
| 4π |
| 6750cos2θsinθ |
| π |
| π |
| 2 |
(Ⅱ)令t=sinθ,t∈(0,1),cos2θ=1-t2,
∴f(t)=
| 6750(t-t3) |
| π |
∴f′(x)=
| 6750(1-3t2) |
| π |
由f′(t)=0,得t=
| ||
| 3 |
| ||
| 3 |
由f′(t)>0,得0<t<
| ||
| 3 |
| ||
| 3 |
∴f(x)在(0,
| ||
| 3 |
| ||
| 3 |
即当t=
| ||
| 3 |
1500
| ||
| π |
点评:本题考查V关于θ的函数关系式的求法,考查函数的定义域的求法,考查圆柱形罐子体积的最大值的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
函数f(x)=(x2-2x-3)(x2-2x-5)的值域是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、[24,+∞) |
| D、(24,+∞) |
已知函数f(
)=x+
-2,则f(x)=( )
| 1 |
| x |
| 1 |
| x |
A、x+
| ||
B、=x+
| ||
C、x+
| ||
D、x+
|
函数y=3x与y=-
的图象关于( )
| 1 |
| 3x |
| A、x轴对称 | B、y轴对称 |
| C、原点对称 | D、直线y=x对称 |
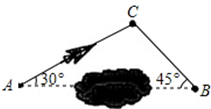 一架飞机从马来西亚吉隆坡飞往中国北京,两地相距4500km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到途中,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程4500km远了多少?(参考数据:
一架飞机从马来西亚吉隆坡飞往中国北京,两地相距4500km.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成30°角的方向飞行,飞行到途中,再沿与原来的飞行方向成45°角的方向继续飞行直到终点.这样飞机的飞行路程比原来的路程4500km远了多少?(参考数据: