题目内容
关于函数f(x)=lg
(x≠0),下列命题错误的是( )
| x2+1 |
| |x| |
| A、f(x)的图象关于y轴对称 |
| B、当x>0时,f(x)是增函数;当x<0时,f(x)是减函数 |
| C、f(x)的最小值是lg2 |
| D、f(x)在区间(2,+∞)上是增函数 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:①定义域为R,又满足f(-x)=f(x),可知函数y=f(x)的图象关于y轴对称;
②令t=x+
(x>0),由函数在(0,1]上是减函数,在[1,+∞)上是增函数,即可判断;
③t=x+
≥2,又是偶函数,即可求得函数f(x)的最小值是lg2;
④当-1<x<0或x>1时函数t=x+
是增函数,根据复合函数知,f(x)是增函数,即可判断.
②令t=x+
| 1 |
| x |
③t=x+
| 1 |
| x |
④当-1<x<0或x>1时函数t=x+
| 1 |
| x |
解答:
解:①定义域为R,又满足f(-x)=f(x),所以函数y=f(x)的图象关于y轴对称,正确.
②令t=x+
(x>0),在(0,1]上是减函数,在[1,+∞)上是增函数,不正确.
③t=x+
≥2,又是偶函数,所以函数f(x)的最小值是lg2,正确.
④当-1<x<0或x>1时函数t=x+
是增函数,根据复合函数知,f(x)是增函数,正确.
故选:B.
②令t=x+
| 1 |
| x |
③t=x+
| 1 |
| x |
④当-1<x<0或x>1时函数t=x+
| 1 |
| x |
故选:B.
点评:本题主要考察了函数单调性的判断与证明,函数的性质及应用,属于基本知识的考查.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知向量
=(-2,2,0),
=(1,0,-1),则它们的夹角是( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |
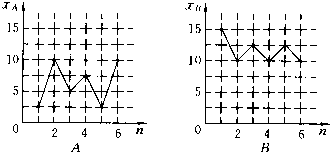
如图:样本A和B分别取自两个不同的总体,他们的样本平均数分别为
A和
B,样本标准差分别为sA和sB,则( )
. |
| x |
. |
| x |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在分别标有号码2,3,4,…,10的9张卡片中,随机取出两张卡片,记下它们的标号,则较大标号被较小标号整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|