题目内容
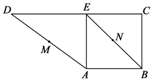如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M、N分别是AD、BE的中点，将三角形ADE沿AE折起，下列说法正确的是①不论D折至何位置（不在平面ABC内）都有MN∥面DEC；
②不论D折至何位置都有MN⊥AE；
③不论D折至何位置（不在平面ABC内）都有MN∥AB．
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：对于说法①，利用线面平行的判定定理，只需证MN平行于平面DEC内的直线DC即可；
对于说法②，由于MN∥DC，要证明MN⊥AE，只需证明AE⊥CD，可转化为证AE⊥平面DEC，由AE⊥EC及AE⊥DE得证．
对于说法③，假设MN∥AB，利用平行公理4逐步推导，得出矛盾，即可判断其正误．
对于说法②，由于MN∥DC，要证明MN⊥AE，只需证明AE⊥CD，可转化为证AE⊥平面DEC，由AE⊥EC及AE⊥DE得证．
对于说法③，假设MN∥AB，利用平行公理4逐步推导，得出矛盾，即可判断其正误．
解答：
解：（1）在直角梯形ABCD中，由BC⊥DC，AE⊥DC，知四边形ABCE为矩形．
连结AC，∵N为BE中点，∴AC过点N．
当D折至某一位置时，如右图所示，连结MN，∵MN为DC中位线，∴MN∥DC，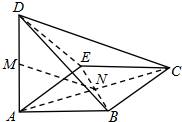
由MN?平面DEC，DC?平面DEC，得MN∥平面DEC．
所以说法①正确．
（2）∵AE⊥EC，AE⊥DE，EC∩DE=E，∴AE⊥平面DEC，又DC?平面DEC，∴AE⊥DC．
由（1）知，MN∥DC，∴MN⊥AE．
所以说法②正确．
（3）假设MN∥AB，由MN∥DC知，DC∥AB，又CE∥AB，得CE∥CD，这与CE∩CD=C相矛盾，
所以假设不成立，即说法③错误．
故答案为①②．
连结AC，∵N为BE中点，∴AC过点N．
当D折至某一位置时，如右图所示，连结MN，∵MN为DC中位线，∴MN∥DC，
由MN?平面DEC，DC?平面DEC，得MN∥平面DEC．
所以说法①正确．
（2）∵AE⊥EC，AE⊥DE，EC∩DE=E，∴AE⊥平面DEC，又DC?平面DEC，∴AE⊥DC．
由（1）知，MN∥DC，∴MN⊥AE．
所以说法②正确．
（3）假设MN∥AB，由MN∥DC知，DC∥AB，又CE∥AB，得CE∥CD，这与CE∩CD=C相矛盾，
所以假设不成立，即说法③错误．
故答案为①②．
点评：本题考查了线面平行的判定定理，线面垂直的定义、判定与性质，平行直线的传递性等，考查了学生的空间想象能力与逻辑推理能力，关键是寻找原图与折起后的图形之间的联系，抓住“变”与“不变”的量．
练习册系列答案
名校课堂系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AC⊥BC，AA1=2，AB=2函数f（x）在定义域R内可导，若f（x）=f（-x），且xf′（x）＜0，设a=f（log47），b=f（log
3），c=f（21.6），则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| A、c＜a＜b |
| B、a＜b＜c |
| C、b＜c＜a |
| D、c＜b＜a |