题目内容
已知函数f(x)=x2-2x+alnx+1有两个极值点x1,x2,且x1<x2.
(1)求实数a的取值范围,并讨论f(x)的单调性;
(2)证明:f(x2)>
.
(1)求实数a的取值范围,并讨论f(x)的单调性;
(2)证明:f(x2)>
| 1-2ln2 |
| 4 |
考点:函数在某点取得极值的条件
专题:计算题,证明题,函数的性质及应用,导数的综合应用
分析:(1)已知函数f(x)=x2-2x+alnx+1有两个极值点x1,x2可化为f′(x)=
=0有两个不同的正根x1,x2,从而解得;再由导数的正负写出函数的单调区间.
(2)由根与系数的关系可得,x1+x2=1,x1x2=
,从而a=2x2(1-x2),代入化简可得f(x2)=(x2-1)2+2x2(1-x2)lnx2,(
<x2<1),令h(t)=(t-1)2+2t(1-t)lnt,(
<t<1),求导判断函数的单调性,从而证明上式成立.
| 2x2-2x+a |
| x |
(2)由根与系数的关系可得,x1+x2=1,x1x2=
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)函数f(x)的定义域为(0,+∞),f′(x)=
,
∵函数f(x)=x2-2x+alnx+1有两个极值点x1,x2,且x1<x2.
∴f′(x)=
=0有两个不同的根x1,x2,且0<x1<x2,
∴
解得,0<a<
,
此时,f(x)在(0,x1)和(x2,+∞)上单调递增,在(x1,x2)上单调递减;
(2)证明:由(1)知,
x1+x2=1,x1x2=
,则a=2x2(1-x2),
因此,f(x2)=(x2-1)2+alnx2=(x2-1)2+2x2(1-x2)lnx2,(
<x2<1)
令h(t)=(t-1)2+2t(1-t)lnt,(
<t<1)则
h′(t)=2(t-1)+[2(1-2t)lnt+2(1-t)]=2(1-2t)lnt,
∵
<t<1,∴1-2t<0,lnt<0,
∴h′(t)>0,
即h(t)在(
,1)上单调递增,
则h(t)>h(
)=
,
即f(x2)>
.
| 2x2-2x+a |
| x |
∵函数f(x)=x2-2x+alnx+1有两个极值点x1,x2,且x1<x2.
∴f′(x)=
| 2x2-2x+a |
| x |
∴
|
解得,0<a<
| 1 |
| 2 |
此时,f(x)在(0,x1)和(x2,+∞)上单调递增,在(x1,x2)上单调递减;
(2)证明:由(1)知,
x1+x2=1,x1x2=
| a |
| 2 |
因此,f(x2)=(x2-1)2+alnx2=(x2-1)2+2x2(1-x2)lnx2,(
| 1 |
| 2 |
令h(t)=(t-1)2+2t(1-t)lnt,(
| 1 |
| 2 |
h′(t)=2(t-1)+[2(1-2t)lnt+2(1-t)]=2(1-2t)lnt,
∵
| 1 |
| 2 |
∴h′(t)>0,
即h(t)在(
| 1 |
| 2 |
则h(t)>h(
| 1 |
| 2 |
| 1-2ln2 |
| 4 |
即f(x2)>
| 1-2ln2 |
| 4 |
点评:本题考查了导数的综合应用,同时考查了根与系数的关系,化简比较繁琐,注意要细心,属于难题.

练习册系列答案
相关题目
函数f(x)在定义域R内可导,若f(x)=f(-x),且xf′(x)<0,设a=f(log47),b=f(log
3),c=f(21.6),则a,b,c的大小关系是( )
| 1 |
| 2 |
| A、c<a<b |
| B、a<b<c |
| C、b<c<a |
| D、c<b<a |
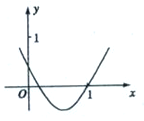 函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
| C、(1,2) | ||||
| D、(2,3) |