题目内容
已知在平面直角坐标系中,点A(1,3),B(3,1),在x轴上求一点C,使△ABC的面积为5.
考点:三角形的面积公式
专题:解三角形
分析:设C(x,0),直线AB的方程为:y-1=
(x-3).利用点到直线的距离公式可得:点C到直线AB的距离d.利用两点之间的距离公式可得|AB|,利用S△ABC=
d|AB|=5,即可得出.
| 3-1 |
| 1-3 |
| 1 |
| 2 |
解答:
解:设C(x,0),
直线AB的方程为:y-1=
(x-3),化为x+y-4=0.
∴点C到直线AB的距离d=
.
|AB|=
=2
.
∴S△ABC=
d|AB|=5,
∴
×2
×
=5,
化为|x-4|=5,
解得x=9或-1.
∴C(9,0)或(-1,0).
直线AB的方程为:y-1=
| 3-1 |
| 1-3 |
∴点C到直线AB的距离d=
| |x-4| | ||
|
|AB|=
| (1-3)2+(3-1)2 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 2 |
| |x-4| | ||
|
化为|x-4|=5,
解得x=9或-1.
∴C(9,0)或(-1,0).
点评:本题考查了点到直线的距离公式、两点之间的距离公式、三角形的面积计算公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
设f(x)=lg
,则f(
)+f(
)的定义域为( )
| 2+x |
| 2-x |
| x |
| 2 |
| 2 |
| x |
| A、(-2,-1)∪(1,2) |
| B、(-4,-2)∪(2,4) |
| C、(-4,0)∪(0,4) |
| D、(-4,-1)∪(1,4) |

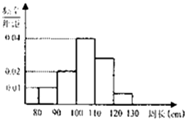 为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是
为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是