题目内容
已知函数f(x)=|2x-1|,a<b<c,且f(a)>f(c)>f(b),则下列结论中成立的是( )
| A、a<0,b<0,c<0 |
| B、a<0,b≥0,c>0 |
| C、2-a<2c |
| D、2a+2c<2 |
考点:指数函数单调性的应用
专题:计算题,函数的性质及应用
分析:根据函数在区间(-∞,0)上是减函数,结合题设可得A不正确;根据函数的解析式,结合举反例的方法,可得到B、C不正确;利用函数的单调性结合函数的解析式,对a<c且f(a)>f(c)加以讨论,可得D是正确的.由此不难得到正确选项.
解答:
 解:对于A,若a<0,b<0,c<0,因为a<b<c,所以a<b<c<0,
解:对于A,若a<0,b<0,c<0,因为a<b<c,所以a<b<c<0,
而函数f(x)=|2x-1|在区间(-∞,0)上是减函数,
故f(a)>f(b)>f(c),与题设矛盾,所以A不正确;
对于B,若a<0,b≥0,c>0,可设a=-1,b=2,c=3,
此时f(c)=f(3)=7为最大值,与题设矛盾,故B不正确;
对于C,取a=0,c=3,同样f(c)=f(3)=7为最大值,
与题设矛盾,故C不正确;
对于D,因为a<c,且f(a)>f(c),说明可能如下情况成立:
(i)a、c位于函数的减区间(-∞,0),此时a<c<0,可得0<2c<2a<1,所以2a+2c<2成立;
(ii)a、c不在函数的减区间(-∞,0),则必有a<0<c,所以f(a)=1-2a>2c-1=f(c),
化简整理,得2a+2c<2成立.
综上所述,可得只有D正确
故选D.
 解:对于A,若a<0,b<0,c<0,因为a<b<c,所以a<b<c<0,
解:对于A,若a<0,b<0,c<0,因为a<b<c,所以a<b<c<0,而函数f(x)=|2x-1|在区间(-∞,0)上是减函数,
故f(a)>f(b)>f(c),与题设矛盾,所以A不正确;
对于B,若a<0,b≥0,c>0,可设a=-1,b=2,c=3,
此时f(c)=f(3)=7为最大值,与题设矛盾,故B不正确;
对于C,取a=0,c=3,同样f(c)=f(3)=7为最大值,
与题设矛盾,故C不正确;
对于D,因为a<c,且f(a)>f(c),说明可能如下情况成立:
(i)a、c位于函数的减区间(-∞,0),此时a<c<0,可得0<2c<2a<1,所以2a+2c<2成立;
(ii)a、c不在函数的减区间(-∞,0),则必有a<0<c,所以f(a)=1-2a>2c-1=f(c),
化简整理,得2a+2c<2成立.
综上所述,可得只有D正确
故选D.
点评:本题以一个带绝对值的函数为例,在已知自变量大小关系和相应函数值的大小关系情况下,叫我们判断几个不等式的正确性,着重考查了函数的图象与单调性等知识点,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
复数
=( )
| 2 |
| 1-i |
| A、1+i | B、1-i |
| C、i | D、1-2i |
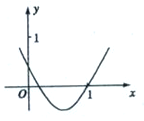 函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
| C、(1,2) | ||||
| D、(2,3) |
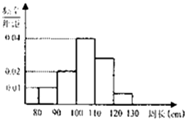 为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是
为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是