题目内容
3.甲、乙、丙三支球队进行某种比赛,其中两队比赛,另一队当裁判,每局比赛结束时,负方在下一局当裁判.设各局比赛双方获胜的概率均为$\frac{1}{2}$,各局比赛结果相互独立,且没有平局,根据抽签结果第一局甲队当裁判(Ⅰ)求第四局甲队当裁判的概率;
(Ⅱ)用X表示前四局中乙队当裁判的次数,求X的分布列和数学期望.
分析 (Ⅰ)第一局无论谁输,第二局都由甲队上场,第四局甲队当裁判(记为事件A),第三局甲队参加比赛(不能当裁判)且输掉(记为事件A2),可知第二局甲队参加比赛且获胜(记为事件A1),A1和A2都发生,A才发生,由此能求出第四局甲队当裁判的概率.
(Ⅱ)由题意S的所有可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(Ⅰ)第一局无论谁输,第二局都由甲队上场,第四局甲队当裁判(记为事件A),
第三局甲队参加比赛(不能当裁判)且输掉(记为事件A2),可知第二局甲队参加比赛且获胜(记为事件A1),
∴A1和A2都发生,A才发生,即P(A)=P(A1A2)=P(A1)P(A2)=$\frac{1}{4}$.
(Ⅱ)由题意S的所有可能取值为0,1,2,
记“第三局乙丙比赛,乙胜丙”为事件A3,“第一局比赛,乙胜丙”为事件B1,
“第二局乙甲比赛,乙胜甲”为事件B2,“第三局比赛乙参加比赛,乙负”为事件B3,
∴P(X=0)=P(B1B2A3)=P(B1)P(B2)P(A3)=$\frac{1}{8}$,
P(X=2)=P($\overline{{B}_{1}}{B}_{3}$)=P($\overline{{B}_{1}}$)P(B3)=$\frac{1}{4}$,
P(X=1)=1-P(X=0)-P(X=2)=$\frac{5}{8}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{8}$ | $\frac{5}{8}$ | $\frac{1}{4}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
14.设函数f(x)=sinωx(ω>0),将f(x)的图象向左平移$\frac{π}{3}$个单位从长度后,所得图象与原函数的图象重合,则ω的最小值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | 6 | D. | 9 |
12.某化工厂有8种产品,由于安全原因,有些产品不允许存放在同一仓库.具体情况由下表给出(“╳”表示该两种产品不能存放在同一仓库)
则该厂至少需要几个产品仓库来存放这8种产品?( )
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | - | ╳ | ╳ | ╳ | ╳ | |||
| 2 | ╳ | - | ╳ | ╳ | ||||
| 3 | ╳ | ╳ | - | ╳ | ╳ | |||
| 4 | ╳ | - | ╳ | |||||
| 5 | ╳ | ╳ | - | ╳ | ||||
| 6 | ╳ | - | ╳ | |||||
| 7 | ╳ | ╳ | ╳ | - | ╳ | |||
| 8 | ╳ | ╳ | - |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
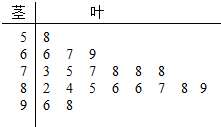 某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.
某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.