题目内容
13.设P为直线3x+4y+3=0上的动点,过点P做圆C:x2+y2-2x-2y+1=0的两条切线,切点分别为A,B,当四边形PACB的面积最小时,∠APB=$\frac{π}{3}$.分析 由题意画出图形,判断四边形面积最小时P的位置,利用点到直线的距离求出PC,然后求出∠P的大小.
解答 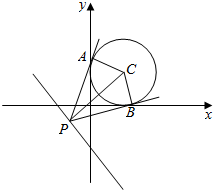 解:圆C:x2+y2-2x-2y+1=0,即圆C:(x-1)2+(y-1)2=1,圆心坐标(1,1),半径为1;
解:圆C:x2+y2-2x-2y+1=0,即圆C:(x-1)2+(y-1)2=1,圆心坐标(1,1),半径为1;
由题意过点P作圆C:x2+y2-2x-2y+1=0的两条切线,切点分别为A,B,
可知四边形PACB的面积是两个三角形的面积的和,因为CA⊥PA,CA=1,
显然PC最小时四边形面积最小,
即PC最小值=$\frac{|3+4+3|}{5}$=2.
sin∠CPA=$\frac{CA}{CP}$=$\frac{1}{2}$,
∴∠CPA=30°,所以∠P=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查直线与圆的位置关系,正确判断四边形面积最小时的位置是解题的关键,考查计算能力.

练习册系列答案
相关题目
1.曲线f(x)=x2上两点A(2,4)和B(2+d,f(2+d))),作割线,当d=0.1时,割线的斜率是( )
| A. | 4 | B. | 4.1 | C. | 4.2 | D. | 4.3 |
18.下列函数中既是奇函数又在区间,[-1,1]上单调递减的是( )
| A. | y=sinx | B. | y=-|x+1| | C. | $y=ln\frac{2-x}{2+x}$ | D. | y=$\frac{1}{2}$(2x+2-x) |
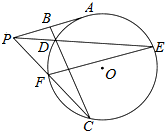 如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证: