题目内容
8．定义在R上的奇函数f（x），当x＞0时，f（x）=2x-x2，则f（-1）=-1．分析 根据函数奇偶性的性质进行转化求解即可．
解答 解：∵f（x）是奇函数，
∴f（-1）=-f（1）=-（2-1）=-1，
故答案为：-1
点评 本题主要考查函数值的计算，利用函数奇偶性的性质进行转化是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
18．下列函数中既是奇函数又在区间，[-1，1]上单调递减的是（ ）
| A． | y=sinx | B． | y=-|x+1| | C． | $y=ln\frac{2-x}{2+x}$ | D． | y=$\frac{1}{2}$（2x+2-x） |
19．已知集合A={x|（x-1）（x+2）＜0}，B={x|-3＜x＜0}，则A∩B=（ ）
| A． | （-∞，-2） | B． | （-2，0） | C． | （0，1） | D． | （1，+∞） |
16．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线平行于直线x+2y+5=0，一个焦点与抛物线y2=-20x的焦点重合，则双曲线的方程为（ ）（ ）
| A． | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B． | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | ||
| C． | $\frac{3{x}^{2}}{25}$-$\frac{3{y}^{2}}{100}$=1 | D． | $\frac{3{x}^{2}}{100}$-$\frac{3{y}^{2}}{25}$=1 |
20．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线方程为$y=\frac{3}{4}x$，则双曲线的离心率为（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{4}{5}$ |
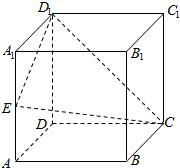如图，有一个正方体的木块，E为棱AA1的中点．现因实际需要，需要将其沿平面D1EC将木块锯开．请你画出前面ABB1A1与截面D1EC的交线，并说明理由．
某食品的保鲜时间t（单位：小时）与储藏温度x（恒温，单位：℃）满足函数关系$t=\left\{\begin{array}{l}64，x≤0\\{2^{kx+6}}，x＞0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时．