题目内容
15.定义在R上的偶函数f(x)在[0,+∞)上的增函数,若f(1)=0,则f(log2x)>0的解集是(0,$\frac{1}{2}$)∪(2,+∞).分析 根据函数的奇偶性和单调性之间的关系,将不等式进行转化,即可得到不等式的解集.
解答  解:∵偶函数f(x)在[0,+∞)上为增函数,f(1)=0,
解:∵偶函数f(x)在[0,+∞)上为增函数,f(1)=0,
∴不等式f(log2x)>0等价为f(|log2x|)>f(1),
即|log2x|>1,
即log2x>1或log2x<-1,
即x>2或0<x<$\frac{1}{2}$,
故不等式的解集为{x|x>2或0<x<$\frac{1}{2}$},
故答案为:(0,$\frac{1}{2}$)∪(2,+∞)
点评 本题主要考查不等式的解法,利用函数的奇偶性和单调性之间的关系是解决本题的关键,综合考查函数性质的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
6.设单位向量$\overrightarrow{e_1}$、$\overrightarrow{e_2}$对于任意实数λ都有|$\overrightarrow{e_1}$+$\frac{1}{2}$$\overrightarrow{e_2}$|≤|$\overrightarrow{e_1}$-λ$\overrightarrow{e_2}$|成立,则向量$\overrightarrow{e_1}$、$\overrightarrow{e_2}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
20.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程为$y=\frac{3}{4}x$,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{5}$ |
7.下列命题中,真命题是( )
| A. | 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 | |
| B. | 若一个平面经过另一个平面的平行线,那么这两个平面相互平行 | |
| C. | 若一条直线平行于一个平面,则这条直线平行于平面内的任意直线 | |
| D. | 若一条直线同时平行于两个不重合的平面,则这两个平面平行 |
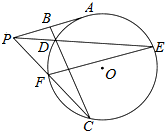 如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证: