题目内容
11.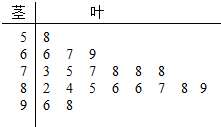 某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.
某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.(Ⅰ)根据样本数据估计A市用户对产品的满意度评分的平均值;
(Ⅱ)根据用户满意度评分,若评分在70分以上(含70分),用户对产品满意,根据所给数据,以事件发生的频率作为相应事件发生的概率,若从A市随机抽取3个用户,记X表示对产品满意的用户个数,求X的分布列及均值.
分析 (Ⅰ)由茎叶图求出样本平均数,由此能估计A市用户对产品的满意度评分的平均值.
(2)记X表示对产品满意的用户个数,X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由茎叶图知:样本平均数为:
$\frac{1}{20}$(50+60×3+70×6+80×8+90×2+8+6+7+9+3+5+7+8×3+2+4+5+6+6+7+8+9+6+8)=80,…(2分)
估计A市用户对产品的满意度评分的平均值约为80分.…(4分)
(2)样本数据中对产品满意的用户为16个,
由题意得,从A市随机抽取一个用户,该用户对产品满意的概率为0.8,
记X表示对产品满意的用户个数,X的可能取值为0,1,2,3,X~B(3,0.8)…(6分)
P(X=0)=${C}_{3}^{0}(1-0.8)^{3}$=0.008,
P(X=1)=${C}_{3}^{1}(1-0.8)^{2}0.8=0.096$,
P(X=2)=${C}_{3}^{2}(1-0.8)0.{8}^{2}$=0.384,
P(X=3)=${C}_{3}^{3}0.{8}^{3}=0.512$,…(8分)
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.008 | 0.096 | 0.384 | 0.512 |
X的均值EX=0×0.008+1×0.096+2×0.384+3×0.512=2.4.…(12分)
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意二项分布的性质的合理运用.

练习册系列答案
相关题目
1.曲线f(x)=x2上两点A(2,4)和B(2+d,f(2+d))),作割线,当d=0.1时,割线的斜率是( )
| A. | 4 | B. | 4.1 | C. | 4.2 | D. | 4.3 |
19.已知集合A={x|(x-1)(x+2)<0},B={x|-3<x<0},则A∩B=( )
| A. | (-∞,-2) | B. | (-2,0) | C. | (0,1) | D. | (1,+∞) |
6.设单位向量$\overrightarrow{e_1}$、$\overrightarrow{e_2}$对于任意实数λ都有|$\overrightarrow{e_1}$+$\frac{1}{2}$$\overrightarrow{e_2}$|≤|$\overrightarrow{e_1}$-λ$\overrightarrow{e_2}$|成立,则向量$\overrightarrow{e_1}$、$\overrightarrow{e_2}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
16.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线平行于直线x+2y+5=0,一个焦点与抛物线y2=-20x的焦点重合,则双曲线的方程为( )( )
| A. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | ||
| C. | $\frac{3{x}^{2}}{25}$-$\frac{3{y}^{2}}{100}$=1 | D. | $\frac{3{x}^{2}}{100}$-$\frac{3{y}^{2}}{25}$=1 |
20.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程为$y=\frac{3}{4}x$,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{5}$ |