题目内容
已知m∈{-1,0,1},n∈{-1,1},若随机选取m,n,则直线mx+ny+1=0恰好不经过第二象限的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:根据古典概型的概率公式求出相应事件的个数,即可得到结论.
解答:
解:由mx+ny+1=0得y=-
x-
,
要使直线mx+ny+1=0恰好不经过第二象限,
则
或者
,
即
或
,
∴n=-1,m=1或n=1,m=0共有2个结果.
∵m∈{-1,0,1},n∈{-1,1},
∴m,n的选择共有3×2=6个结果,
则根据古典概率的概率公式得所求的概率P=
=
,
故答案为:
| m |
| n |
| 1 |
| n |
要使直线mx+ny+1=0恰好不经过第二象限,
则
|
|
即
|
|
∴n=-1,m=1或n=1,m=0共有2个结果.
∵m∈{-1,0,1},n∈{-1,1},
∴m,n的选择共有3×2=6个结果,
则根据古典概率的概率公式得所求的概率P=
| 2 |
| 6 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题主要考查古典概型的概率的计算,根据直线不经过第二象限,分别求出对应斜率和截距的关系是解决本题的关键,比较基础.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
设函数f(x)=
的定义域为M,则∁RM=( )
| 1 | ||
|
| A、(-∞,1) |
| B、(1,+∞) |
| C、(-∞,1] |
| D、[1,+∞) |
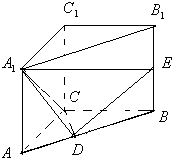 已知直三棱柱ABC-A1B1C1中,∠ACB=
已知直三棱柱ABC-A1B1C1中,∠ACB=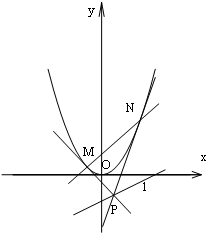 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示