题目内容
设函数f（x）=
的定义域为M，则∁RM=（ ）
| 1 | ||
|
| A、（-∞，1） |
| B、（1，+∞） |
| C、（-∞，1] |
| D、[1，+∞） |
考点：补集及其运算,函数的定义域及其求法
专题：集合
分析：根据函数成立的条件，求出函数的定义域，然后根据补集的定义即可得到结论．
解答：
解：要使函数f（x）=
有意义，则1-x＞0，即x＜1，
∴函数的定义域M=（-∞，1），
则∁RM=[1，+∞），
故选：D．
| 1 | ||
|
∴函数的定义域M=（-∞，1），
则∁RM=[1，+∞），
故选：D．
点评：本题主要考查集合的基本运算，利用函数成立的条件求出函数的定义域是解决本题的关键，比较基础．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
在区间[-2，2]上随机取一个数m，则直线y=x+m与圆x2+y2=2x相交的概率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知三点A（2，1），B（1，-2），C（
，-
），动点P（a，b）满足0≤
•
≤2，且0≤
•
≤2，则点P到点C的距离大于
的概率为（ ）
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
一简单组合体的三视图如图所示，则该组合体的体积为（ ）
| A、16-π | B、12-4π |
| C、12-2π | D、12-π |
已知集合A={x|x2-x＜0}，集合B={x|2x＜4}，则“x∈A”是“x∈B”的（ ）
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某几何体的三视图如图所示（单位：cm），则该几何体的体积是（ ）
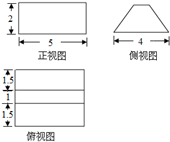
A、
| ||
| B、50cm3 | ||
C、
| ||
| D、25cm3 |
设a=log210，b=log315，c=log735，则（ ）
| A、c＞a＞b |
| B、b＞c＞a |
| C、b＞a＞c |
| D、a＞b＞c |