题目内容
18.已知i为虚数单位,则复数$\frac{1}{1+i}$在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出.
解答 解:复数$\frac{1}{1+i}$=$\frac{1-i}{(1+i)(1-i)}$=$\frac{1}{2}-\frac{1}{2}$i在复平面内对应的点$(\frac{1}{2},-\frac{1}{2})$位于第四象限.
故选:D.
点评 本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
8.已知集合A={x∈N|-1<x<5},B={x|-x2+5x+6>0},则A∩B=( )
| A. | {-1,0,1,3} | B. | {-1,0,1,2} | C. | {-1,0,1} | D. | {0,1,2,3,4} |
13.过点(1,2)且与直线y=2x+1垂直的直线的方程为( )
| A. | x+2y-3=0 | B. | 2x-y+4=0 | C. | x+2y+3=0 | D. | x+2y-5=0 |
10.过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,且|AF|=2|BF|,则直线AB的斜率为( )
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$或$-2\sqrt{2}$ | D. | $2\sqrt{3}或-2\sqrt{3}$ |
7.过抛物线y2=4x的焦点F且斜率为$2\sqrt{2}$的直线交抛物线于A,B两点(xA>xB),则$\frac{{|{AF}|}}{{|{BF}|}}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | 3 | D. | 2 |
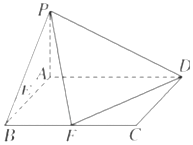 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.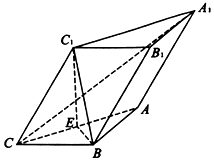 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.