题目内容
3.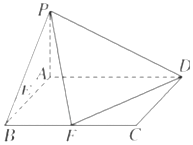 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.(1)证明:PF⊥FD;
(2)若PA=1,求点E到平面PFD的距离.
分析 (1)连接AF,通过计算利用勾股定理证明DF⊥AF,证明DF⊥PA,推出DF⊥平面PAF,然后证明DF⊥PF.
(2)利用等体积方法,求点E到平面PFD的距离.
解答 (1)证明:连接AF,则AF=$\sqrt{2}$,DF=$\sqrt{2}$,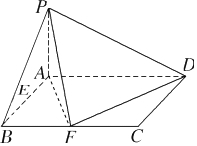
又AD=2,∴DF2+AF2=AD2,∴DF⊥AF,
又PA⊥平面ABCD,∴DF⊥PA,又PA∩AF=A,
∴DF⊥平面PAF,
又PF?平面PAF,
∴DF⊥PF.
(2)解:∵S△EFD=2-$\frac{5}{4}$=$\frac{3}{4}$,
∴VP-EFD=$\frac{1}{3}×\frac{3}{4}×1$=$\frac{1}{4}$,
∵VE-PFD=VP-AFD,
∴$\frac{1}{3}×\frac{\sqrt{6}}{2}h=\frac{1}{4}$,解得h=$\frac{\sqrt{6}}{4}$,即点E到平面PFD的距离为$\frac{\sqrt{6}}{4}$.
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,点到平面的距离距离的求法,考查计算能力以及空间想象能力.

练习册系列答案
相关题目
13.在△ABC中,AH⊥BC于H,点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$,若|$\overrightarrow{AH}$|=$\sqrt{2}$,则$\overrightarrow{AH}$•$\overrightarrow{AD}$=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
14.设a=sin$\frac{π}{5}$,b=log${\;}_{\sqrt{2}}$$\sqrt{3}$,c=($\frac{1}{4}$)${\;}^{\frac{2}{3}}$,则( )
| A. | a<c<b | B. | b<a<c | C. | c<a<b | D. | c<b<a |
11.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”,已知“日减功迟”的具体含义是每天比前一天少织同样多的布,则此问题的答案是( )
| A. | 10日 | B. | 20日 | C. | 30日 | D. | 40日 |
18.已知i为虚数单位,则复数$\frac{1}{1+i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.已知圆C1:x2+y2=4,圆C2:x2+y2+6x-8y+16=0,则圆C1和圆C2的位置关系是( )
| A. | 相离 | B. | 外切 | C. | 相交 | D. | 内切 |
13.将一颗骰子掷两次,则第二次出现的点数是第一次点数的2倍的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |