题目内容
8.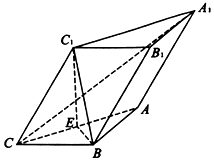 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.(1)求证:A1C⊥平面C1EB;
(2)求直线CC1与平面ABC所成角的余弦值.
分析 (1)证明BE⊥平面A1ACC1,可得BE⊥A1C,即可证明:A1C⊥平面C1EB;
(2)判断∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,即可求直线CC1与平面ABC所成角的余弦值.
解答 (1)证明:∵AB=BC,E为AC的中点,∴BE⊥AC,
∵平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC=AC,
∴BE⊥平面A1ACC1,
∵A1C?平面A1ACC1,∴BE⊥A1C.
又BC1⊥A1C,BE∩BC1=B,∴A1C⊥面C1EB.
(2)解:∵面A1ACC1⊥面ABC,∴C1在面ABC上的射影H在AC上,
∴∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,
在Rt△C1CM中,CM=CC1cos∠C1CM=2cos60°=1.
在Rt△CMH中,$CH=\frac{CM}{cos∠ACB}=\frac{{2\sqrt{3}}}{3}$.
∴在Rt△C1CH中,$cos∠{C_1}CH=\frac{CH}{{C{C_1}}}=\frac{{\frac{2}{3}\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{3}$.
∴直线C1C与面ABC所成的角的余弦值为$\frac{{\sqrt{3}}}{3}$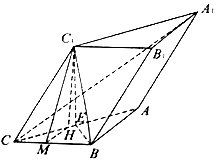
点评 本题考查线面垂直的判定与性质,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知i为虚数单位,则复数$\frac{1}{1+i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.“x2+5x-6>0”是“x>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知实数x,y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ x+2y≤4\\ x-2y≤2\end{array}\right.$,如果目标函数z=x+ay的最大值为$\frac{16}{3}$,则实数a的值为( )
| A. | 3 | B. | $\frac{14}{3}$ | C. | 3或$\frac{14}{3}$ | D. | 3或$-\frac{11}{3}$ |
3.已知函数f(x)满足f($\frac{1}{x}$)+$\frac{1}{x}$f(-x)=2x(x≠0),则f(-2)=( )
| A. | $-\frac{7}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{7}{2}$ | D. | $-\frac{9}{2}$ |
13.将一颗骰子掷两次,则第二次出现的点数是第一次点数的2倍的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
17.若圆x2+y2-2x-4y+1=0关于直线ax-by=0(a>0,b>0)对称,则双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1的渐近线方程为( )
| A. | y=2x | B. | $y=\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{2}x$ |