题目内容
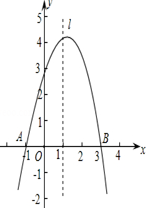 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
考点:二次函数的性质
专题:分类讨论,函数的性质及应用
分析:(1)把三个点的坐标代入解析式,解方程组求得a、b、c,即可得抛物线的函数关系式;
(2)根据抛物线的对称性,PA+PC=PB+PC,当P在直线BC上时△PAC的周长PA+PC+AC最小,求出直线BC与对称轴的交点坐标,即得P的坐标;
(3)设M(1,m),△MAC为等腰三角形,分①MA=MC;②MA=AC;③MC=AC,讨论求解.
(2)根据抛物线的对称性,PA+PC=PB+PC,当P在直线BC上时△PAC的周长PA+PC+AC最小,求出直线BC与对称轴的交点坐标,即得P的坐标;
(3)设M(1,m),△MAC为等腰三角形,分①MA=MC;②MA=AC;③MC=AC,讨论求解.
解答:
 解:(1)将A(-1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c中,得:
解:(1)将A(-1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c中,得:
,
解得
,
∴抛物线的解析式:y=-x2+2x+3.
(2)连接BC,直线BC与直线l的交点为P;
根据抛物线的对称性,PA+PC=PB+PC,当P在直线BC上时△PAC的周长PA+PC+AC最小,
设直线BC的解析式为y=kx+b,将B(3,0),C(0,3)代入上式,得:
,解得:
∴直线BC的函数关系式y=-x+3;当x=1时,y=2,
即P的坐标(1,2).
(3)抛物线的解析式为:x=-
=1,
设M(1,m),已知A(-1,0)、C(0,3),则:
MA2=m2+4,MC2=m2-6m+10,AC2=10;
①若MA=MC,则MA2=MC2,得:m2+4=m2-6m+10,得:m=1;
②若MA=AC,则MA2=AC2,得:m2+4=10,得:m=±
;
③若MC=AC,则MC2=AC2,得:m2-6m+10=10,得:m=0,m=6;当m=6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,
),(1,-
),(1,1),(1,0).
 解:(1)将A(-1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c中,得:
解:(1)将A(-1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c中,得:
|
解得
|
∴抛物线的解析式:y=-x2+2x+3.
(2)连接BC,直线BC与直线l的交点为P;
根据抛物线的对称性,PA+PC=PB+PC,当P在直线BC上时△PAC的周长PA+PC+AC最小,
设直线BC的解析式为y=kx+b,将B(3,0),C(0,3)代入上式,得:
|
|
∴直线BC的函数关系式y=-x+3;当x=1时,y=2,
即P的坐标(1,2).
(3)抛物线的解析式为:x=-
| b |
| 2a |
设M(1,m),已知A(-1,0)、C(0,3),则:
MA2=m2+4,MC2=m2-6m+10,AC2=10;
①若MA=MC,则MA2=MC2,得:m2+4=m2-6m+10,得:m=1;
②若MA=AC,则MA2=AC2,得:m2+4=10,得:m=±
| 6 |
③若MC=AC,则MC2=AC2,得:m2-6m+10=10,得:m=0,m=6;当m=6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,
| 6 |
| 6 |
点评:本题考查了函数解析式的求法,二次函数的图象性质,体现了数形结合思想与分类讨论思想.

练习册系列答案
相关题目
已知x0是函数f(x)=(
)x-
的一个零点,若x1∈(0,x0),x2∈(x0,+∞),则( )
| 1 |
| 2 |
| x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)>0,f(x2)<0 |
| C、f(x1)<0,f(x2)>0 |
| D、f(x1)>0,f(x2)>0 |
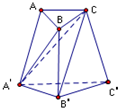 如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )
如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )| A、1:1:1 |
| B、2:1:1 |
| C、4:2:1 |
| D、4:4:1 |
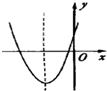 二次函数y=ax2+bx+c的图象如图所示,则a+b+c
二次函数y=ax2+bx+c的图象如图所示,则a+b+c 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=