题目内容
某商品在近30天内每件的销售价格P(元)和时间t(天)的函数关系为:P=
(t∈N*),设商品的日销售量Q(件)与时间t(天)的函数关系为Q=40-t(0<t≤30,t∈N*),则第 天,这种商品的日销售金额最大.
|
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:分情况讨论即可获得日销售金额y关于时间t的函数关系式,根据分段函数不同段上的表达式,分别求最大值最终取较大者分析即可获得问题解答.
解答:
解:由题意得:y=
.
当0<t<25,t∈N*时,y=(t+20)(40-t)=-t2+20t+800=-(t-10)2+900.
∴t=10(天)时,ymax=900(元),
当25≤t≤30,t∈N*时,y=(-t+100)(40-t)=t2-140t+4000=(t-70)2-900,
而y=(t-70)2-900,在t∈[25,30]时,函数递减.
∴t=25(天)时,ymax=1125(元).
∵1125>900,
∴第25天日销售额最大为1125元.
故答案为:25.
|
当0<t<25,t∈N*时,y=(t+20)(40-t)=-t2+20t+800=-(t-10)2+900.
∴t=10(天)时,ymax=900(元),
当25≤t≤30,t∈N*时,y=(-t+100)(40-t)=t2-140t+4000=(t-70)2-900,
而y=(t-70)2-900,在t∈[25,30]时,函数递减.
∴t=25(天)时,ymax=1125(元).
∵1125>900,
∴第25天日销售额最大为1125元.
故答案为:25.
点评:本题考查分段函数的应,考查分类讨论的思想、二次函数求最值得方法以及问题转化的能力,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
过点M(-1,m),N(m+1,4)的直线的斜率等于1,则m的值为( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
一几何体的三视图如图所示,圆的半径均为2,则该几何体的 表面积( )
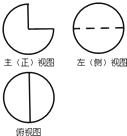

| A、16π | B、14π |
| C、12π | D、8π |
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的
,且样本容量为200,则中间一组有频数为( )
| 1 |
| 4 |
| A、40 | B、32 |
| C、0.2 | D、0.25 |
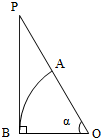 如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
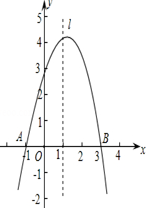 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.